Site map of:
E = γmc2
I2 = (ct)2 – x2 = (ct´)2 – x´2 =…
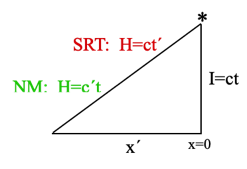
NM: Vwrt x=0 = (x´/t) = (x´/I)c
SRT: vwrt x=0=(x´/t´)=(x´/H)c
NM: Vwrt* = (H/t) = (c´t)/t = c´
SRT: vwrt * = (H/t´) = (ct´/t´) = c
Relativistic vs. Newtonian Kinetic Energy
Dr. Sherwood Kaip
El Paso, TX
<skaip799@gmail.com>; cell: 1 (915) 309-6340
This material may be reproduced if author attribution is given.
To return from PRINT page, click "back" arrow on your browser
Abstract
The value of the kinetic energy of a moving body of momentum P is not the same value in Special Relativity (SRT) as it is in Newtonian Mechanics (NM). This paper examines, explains, and corrects this dilemma using two methods.
Kinetic Energy in SRT and NM
Kinetic energy of a freely moving body, which will be denoted by KS in SRT and KN in NM, is the product of the force F applied times the distance x´ over which it is applied, or
K = F x´ 1
Net applied force results in change in momentum P .
F = dP/dt 2
So
KS = (dP/dt)x´ 3
in SRT. Also, NM kinetic energy must equal
KN = (dP/dt)x´ 4
In SRT
I2 = (ct)2 – x2 = (ct´)2 – x´2 = … 5
where I is the Relativistic Interval Equation which is the same in all reference frames for any two events, c is the speed of light, and t in these examples is the time during which the light originating in the non-moving reference frame at x=0 has traveled the distance I at speed c in that frame. The x´ is the distance an object or reference frame has moved perpendicularly while the light has moved the distance I . The x=0 when considering the light rays moving perpendicular to the direction of motion of x´ . Then the formula looks like
I2 = (ct)2 = (ct´)2 – x´2 = (ct´´)2 – x´´2 … 6
The x (not x´ ) in these examples will not change because it is the non-moving reference frame, x=0 .
Speed is distance per unit time. If you know the distance an object traveled, x´ , the distance a timing signal (light) traveled, I , and the speed, c , of that timing signal, then NM velocity, V , would be
V = (x´/I)c = (x´/ct)c = x´/t 7
Momentum P in NM is
P = mV = m(x´/t) = m(x´/I)c 8
According to SRT
x´= γ(x+vt) 9
t´ = γ(t + (v/c2)x) 10
so for x=0 , in which case I=ct ,
x´= γvt = γ(v/c)ct = γ(v/c)I 11
t´ =γt 12
where x´ is the distance the moving frame traveled while the light traveled the distance I at speed c , γ is the gamma function, γ=1/(1 – (v/c)2)1/2 , t´ is calculated from (I/c) according to the SRT Eq. 12, and v is the SRT velocity (not the same as NM velocity V ), which is x´/t´ by dividing Eq. 11 by Eq. 12 or
x´/t´ = γvt/γt = v 13
By Eq. 11
x´/I = γ(v/c) 14
and momentum P in SRT has the same value as in NM, namely
P = m(x´/I)c = mγ(v/c)c = mγv 15
using Eqs. 8 and 14. Since in NM P=mV , then
V = γv 16
x´/I = (γv)/c = γ(v/c) = (P/m)/c 17
meaning the ratio of the distance the object traveled to the distance the light traveled is (P/m)/c . Therefore, distance traveled x´ would be
x´ = (P/m)I/c = (1/m)Pct/c = (1/m)Pt . 18
However, P is varying at the rate (dP/dt) = F = a constant. P at any given time is
P = (dP/dt)t 19
Using Eqs. 18 and 19
dx´ = (1/m)(dP/dt)t dt 20
x´ = (1/m)(dP/dt) ∫t dt 21
x´ = (1/2m)(dP/dt) t2 22
and since K=Fx´ , from Eqs. 3 and 22 one gets
KS = (dP/dt) x´ = (1/2m) (dP/dt)2 t2 23
which is
KS = (1/2m) (m d(γv)/dt)2 t2 = ½ m(γv)2 24
in SRT. In NM it is
KN = (1/2m) (m dV/dt)2 t2 = ½ mV2 25
Another Method
The usual formula given for KS in SRT is
KS = mc2 (γ–1) . 26
This is derived from
dK = F dx´ = (dP/dt) dx´ = (dx´/dt) dP . 27
The correct P=mγv was used for the P of dP . However, the (dx´/dt) which equals P/m , the correct form and the same as NM velocity, is not what was used for the integration. Instead, P/γm was used for (dx´/dt) which is v or (dx´/dt´ ) , where the denominator is the dilated time, was used. Thus the integration result of mc2(γ–1) for KS .
If calculated correctly by this “(dx´/dt) dP” method of Eq. 27, it looks like this.
dKS = F dx´ = (dP/dt) dx´ = (dx´/dt) dP = (1/m) P dP 28
KS = (1/m) ∫PdP 29
Therefore, by the method used to calculate the “(γ-1)” version (Eq. 27) for KS , when done properly using (1/m)P instead of (1/m)(P/γ)=v , the result is
KS = (1/2m) P2 = ½ m(γv)2 = ½ mc2(γ(v/c))2 30
just as found above in Eq 24. Which, by the way, since P=mV in NM, is
KN = (1/2m) P2 = ½ mV2 = ½ mc2(V/c)2 = ½ mc2(γ(v/c))2 31
Conclusion
The correct equation for kinetic energy in Special Relativity (SRT) is
KS = ½ m(γv)2 = ½ mc2(γ(v/c))2 = ½ mc2(V/c)2
equal to the Newtonian Mechanics (NM) value
KN =½ mV2 = ½ mc2(V/c)2
The difference between the old KS=mc2(γ–1) and the correct KS= ½ m(γv)2 = ½ mc2(γ(v/c))2 is < 1% for
(v/c) < 0.2 .