Site map of:

                  SRT Overview

     Encryption          NM from SRT

     SRT where why  E=mc2 flawed

        Interval              Rest Mass

        Algebra                E not saved

        SR < > NM            SRT vs. NM E

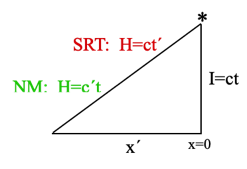
NM:   Vwrt x=0 = (x´/t) = (x´/I)c

SRT:   vwrt x=0=(x´/t´)=(x´/H)c

NM:   Vwrt* = (H/t) = (c´t)/t = c´

SRT:   vwrt * = (H/t´) = (ct´/t´) = c

Abstract

     Collision problems are often discussed in terms of momentum  (P) and kinetic energy, either  K=(γ–1)mc2  for Special Relativity Theory (SRT) or  K=(½)mV2  for Newtonian Mechanics (NM).  However, collision problems can be solved using only momentum  (P) and mass  (m) and ignoring ‘kinetic energy’.  By doing this, the equations are the same in SRT as in NM.  

     Also shown is that SRT kinetic energy is characteristically not conserved in elastic collisions.

Solving Collisions without Kinetic Energy

     In one dimension, a ‘collision’ is the result of the application of a force in equal and opposite directions on two objects,  m1  and  m2 , which are moving at  P1/m1  and  P2/m2  respectively for a period of time  t , coming closer together, until both objects are moving together at

P3/(m1+m2) = (P1+P2)/(m1+m2).

Change of momentum of free objects is the result of a force  (F) acting for a time  (t)  , i.e.,  dP=Fdt .  It can be a small force acting over a long time or a large force acting over a correspondingly short time.  The force causes momentum added to one object to be subtracted from the other until they are both moving at the same speed with respect to the observer and not moving with respect to each other at collision.  The total momentum  P1+P2  remains constant.  If the ‘collision’ is inelastic, that is the final stage.  They have each lost all their kinetic energy and velocity relative to each other and to some reference frame, called the center of momentum reference frame, and travel together at the same speed in other reference frames.  

     If the same amount of momentum change  dP=Fdt  is again applied, they will wind up moving away from each other.  If a perfectly elastic collision, the objects, which started out moving at  

((P1/m1) – (P2/m2)) = S

with respect to each other, will wind up at

[(P2/m1) – (P5/m2)] = (–)[(P1/m1) – (P2/m2)] = (–) S

moving away from each other where  P2  and  P5  are the new after collision momenta of the first and second objects, respectively.  Let

P1 + P2 = PT    ,  

((P1/m1) – (P2/m2)) = S              

m1 + m2 = mT    .

If  S  is positive, (the positive direction is from  m1  to  m2 )  the objects are moving toward each other to collision.  If  S  is negative, they are moving apart.  The first object that was formerly moving at  (P1/m1) will now be moving at

(P2/m1) =  (PT – m2S) / mT  = [P1(1 – (m2/m1)) + 2P2] / (m1 + m2)

and the second object, formerly moving at  (P2/m2) ,  will now be moving at

(P5/m2) =  (PT + m1S) / mT  = [P2(1 – (m11/m2)) + 2P1] / (m1 + m2)

or, more easily,

(P5/m2) = (P2/m1) + S  

Now

(P2/m1) – (P5/m2) = (–) [(P1/m1) – (P2/m2)].

     Actually, both momenta are not needed to solve the collision problem.  All that is needed is the value of S  and the value of the two masses, in which case  PT= 0 and the calculations are for a center of momentum reference frame..  Then you can pick any value for one initial momentum and calculate the needed value of the other.

P2 = m2((P1/m1) – S)    .  

P1 = m1((P2/m2) + S)    

If the two momenta are not equal and opposite, i.e. P1+P2≠0 ,  it means that the approach to collision is being observed and measured from a non-center-of-momentum reference frame.  However,

P1 = – P2 = m1m2S / mT  

will give the values for observing from a center of momentum reference frame where  P1+P2=0 .

     Any number (including negative) can be added to both  (P1/m1)  and  (P2/m2) .  It will represent an observer moving at a different speed relative to the objects that are colliding.

     This full analysis of elastic and inelastic collisions has been done using only the concepts of mass  m  and momentum  P and the results are the same for both SR and NM, keeping in mind that  (P/m)=V  in NM and  γv  in SRT.  (The SRT velocity,  v ,  and the NM velocity,  V ,  are never the same but are related by  V=γv  .)  Kinetic energy concepts were not used.

Kinetic Energy in SRT Collisions

     However, the usual way to examine collisions is to say that, in elastic collisions, both momentum and kinetic energy,  K=½ mV2 in NM and  KR=mc2(γ – 1) in SRT, are conserved.  This works easily for NM where the kinetic energy lost in the objects coming to a stop relative to each other is said to be converted to ‘potential energy’ which is available to restore the objects to the same speed relative to each other but in the opposite direction.  Using the methods above for NM, kinetic energy will be found to be conserved.

     However, in SRT, while momentum  P  is also conserved, kinetic energy,  KR=mc2(γ – 1)  (Relativistic kinetic energy)  will not generally be conserved in a collision, i.e., in general                    

K1 + K2 ≠ K2 + K5

     In SRT, momentum  P  is conserved.  The following is the equation P1+P2=P2+P5 divided by the constant  c

m1 [ (P/mc)1 – (P/mc)2 ]=  m2 [ (P/mc)5 – (P/mc)2 ]     .

  This can also be written in the unusual form

m1[ ((P/mc)12)1/2 – ((P/mc)22)1/2 ]  =  m2 [ ((P/mc)52)1/2 – ((P/mc)22)1/2 ]    .

Any number added to or subtracted from each of the above four terms would not affect the equation’s equality.      

     Relativistic potential energy  KR ,  which is claimed to be conserved, can also be written in terms of mass and momentum,  P=mγv .  Relating  γ  to  m and  P ,

γ 2 = 1/(1 – (v/c)2 )   ;     γ2 – γ2(v/c)2 = 1    ;    γ2 = (P/mc)2 + 1

Thus, the formula for  Relativistic kinetic energy  KR=mc2(γ– 1)  can be written

KR/c2 = m [((P/mc)2 + 1)1/2 – 1]    .     

So, if Relativistic kinetic energy is conserved

K1/c2 – K2/c2 = K5/c2 – K2/c2

and therefore

m1 [((P/mc)12 + 1)1/2  – ((P/mc)22 + 1)1/2 ] ?=? m2 [((P/mc)52 + 1)1/2  – ((P/mc)22 + 1)1/2 ]    

where the  “ –1’s “  have canceled out, must also be true.

     This kinetic energy equation is the same as the correct ‘momentum conservation’ equation above, i.e.,  (m1[ ((P/mc)12)1/2 –  …) ,  except for the  “ +1 “  in the square root terms.  If the  “ +1 “  added the same amount to each term, the equation would still balance, but it doesn’t.  If there are four different numeric values for the variables  m1, m2, P1, P2,  then  P2   and  P5  will be different from  P1  and  P2 .  This will result in a different amount being added to each of the four correct  ((P/mc)2)½  terms (equivalent to  P/mc )  and will make the two sides of the  K1–K2=K5–K2  equation unequal, demonstrating that SRT kinetic energy is generally not conserved.  

     However, there are three instances in which the SRT kinetic energy equation will be correct.  If  m1  equals  m2 ,  V2=V2  and  V5=V1 ,  resulting in equal additions to both sides.  If  P1 + P2 = 0 ,  this also occurs.  The third instance is when  P1  or P2  = zero.  This occurs when one of the masses is fixed in place in a reference frame.  Since the moving object will simply reverse course at the same speed, the before and after  Kr’s  will be equal.     Other than these three instances, the SRT kinetic energy equation does not balance and is therefore inaccurate.

     Some have tried changing masses to make the equation balance but the problem with that is that the mass corrections change for different observers moving at different speeds relative to the colliding masses.

Summary

     Collision problems can be solved using only momentum  P  and mass  m  without invoking kinetic energy.  The problems will work out the same in NM and SRT because momentum and mass (rest mass if you prefer) are numerically the same in both SR and NM.  In NM,  P=mV  and in SRT  P=mγv .  Thus,  V=γv  and  (V/c)=γ(v/c) .  

     In elastic collisions, kinetic energy is conserved in NM.  In SRT, kinetic energy  KR=mc2(γ – 1)  is conserved only in three instances: a center of momentum reference frame (i.e.,   P1+P2=0 ),  when the colliding masses are equal  (m1=m2) ,  or one object does not change momentum as the result of the collision, such as by being fixed in place in its reference frame.

Kinetic Energy is Characteristically

Not Conserved in Special Relativity (SRT)

Elastic Collisions

Dr. Sherwood Kaip

El Paso, TX

<skaip799@gmail.com>;   cell: 1 (915) 309-6340

This material may be reproduced if author attribution is given.