Site map of:
E = γmc2
I2 = (ct)2 – x2 = (ct´)2 – x´2 =…
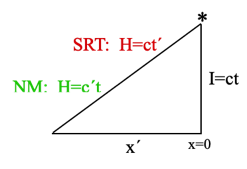
NM: Vwrt x=0 = (x´/t) = (x´/I)c
SRT: vwrt x=0=(x´/t´)=(x´/H)c
NM: Vwrt* = (H/t) = (c´t)/t = c´
SRT: vwrt * = (H/t´) = (ct´/t´) = c
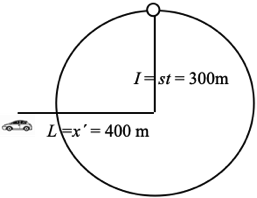
Consider a timing signal which left the center of the circle one second ago and is now the distance 300m at the periphery of the 300 meter circle. The speed of the timing signal has been checked many times and is always 300 meters per second from its source, the center of the circle, wherever that may be. Consider also an object (the car) which passed by the center of the circle 1 second ago and has traveled the distance
L=x´=400 meters. Therefore, the timing signal has a speed s of 300 meters/sec and the object has a speed V=400 meters/sec (m/s) relative to the center of the circle. This could also be written as
V = (L/t) = (x´/t) = (x´/I)s = 400 m/s ; V = (4/3) s
for the object relative to the source of the timing signal, the center of the circle.
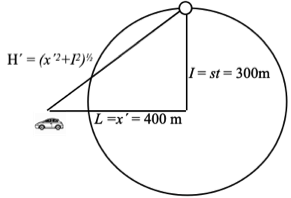
Now, what distance has the object (car) traveled with respect to the part of the timing signal which traveled perpendicular to the object’s motion? This distance would be H´ which is
H´ = (x´2+I2)1/2 .
So the speed of the object with respect to the perpendicular portion of the timing signal would be
H´/t = (x´2+I2)1/2 / t = [(x´2 + I2)½/I ] s = (H´/I)s
Of course, this speed H´/t is always greater than s because distance H´ is always greater than distance I=st . Call this speed s´ .
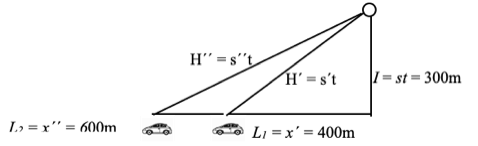
Above shows a second object (car) which passed the circle’s center at the same time as the first but at a higher speed as shown by the greater distance it has traveled during the one second. There could be very many other objects at different speeds. However, a simple formula connects all these events.
I2 = H2 - x2 = H´2 - x´2 = H´´2 - x´´2 =… = (st)2 - x2 = (s´t)2 - x´2 = (s´´t)2 - x´´2 =…
This is the Interval equation for Newtonian Mechanics (NM). Variables from this formula can be used to derive the usual NM transformation
∆x = x´ – x = Vt
where x is the original displacement from zero in the non-moving reference frame. This analysis would be the same if the time were changed to 1.0 millisecond, 1.0 microsecond (where s would be the speed of light, c ), or 1.0 nanosecond. This straightforward analysis covers NM. How would this same situation look in Special Relativity Theory (SRT)?
According to SRT light travels the same speed c relative to all things. This is the meaning of Einstein’s second postulate. In the above example, then light must travel at the same speed relative to the moving object (car) as it does relative to its source at the center of the circle. Equivalently in the above example this would mean that s´=s . Obviously H´≠st because H´>I . And in SRT H´≠ct because H´>I . In SRT this is ‘solved’ by saying that time t in the moving reference frame of the object (car) changed so as to make the formula H´=st´ (H´=ct´) . What creates SRT is insisting that s´=s , whether or not s is the speed of light c . All other values, including that of H´ , remain the same. All instances of variable s can now be replaced by c . The SRT Interval formula now reads
I2 = H2 – x2 = H´2 – x´2 = H´´2 – x´´2 =… = (ct)2 – x2 = (ct´)2 – x´2 = (ct´´)2 – x´´2 =… .
Since the new time t´ (or t´´ or t´´´, etc.) is related to the moving reference frame of the object, it is used to now make the SRT speed v of the object relative to the center of the circle
v = (L/t´) = (x´/t´) = (x´/H´)s = 240 m/s ; v = (4/5) s
Note the difference between the NM velocity V and the SRT velocity v . Nothing can go faster than light according to SRT because v/s=(x´/H´)s/s=x´/(x´2+I2)1/2 , a number that will always be less than 1.0.
All the equations and concepts of SRT can be derived from the SRT Interval equation which results from the error of claiming that something, light or, in this case, the timing signal, moves at the same speed with respect to two things which are moving with respect to each other. Obviously the timing signal (or light) is not moving at the same speed with respect to its source as it is with respect to the object.
Multiplying the SRT Interval equation (ct´)2 –x´2=I2 by (mc/t)2 results in the well known SRT equation
E2 – (Pc)2 = (mc2)2 .
The derivation is not included here. The often used SRT factor gamma, γ , is
γ = (H´/I) = (ct´)/(ct) [SRT] = (c´t)/(ct) [NM]
γ2 = (H´/I)2 = (ct´)2 / ((ct´)2 – x´2) = 1 / (1 – x´2/(ct´)2) = 1 / (1 – (v/c)2) ,
the usual formula for γ2 . The transformation equations of SRT convert directly into the SRT Interval equation.
x´ = γ(vt + x) ; x´ = γ(v/c)ct + γx
t´ = γ(t + (v/c2)x ; ct´ = γct + γ(v/c)x
I2 = (ct´)2 – x´2 = [γct + γ(v/c)x]2 – [γ(v/c)ct + γx]2 = (ct)2 – x2
SRT total energy is E= γmc2 . If the SRT Interval equation is multiplied by (γmc/t´)2 ,
(γmc/t´)2 (ct´)2 = E2 = (γmc/t´)2 (I2 + x´2) = (γmc/t´)2 (ct´)2 = (γmc2)2 ; E = γmc2
which is the correct form, according to SRT, of Einstein’s famous equation. (Since everything has nearly infinite velocities, depending on what you are comparing it to, the original erroneous E=mc2 would give innumerable different masses for every object.)
Fortunately, any SRT depiction can be converted into one and only one correct equivalent NM description (and vice versa). This has been written up by the author as “SRT to NM and vice versa”. As shown above, if v=0.8c , then V=γv=(4/3)c and for every 300 m the light travels, the object travels 400 m, just as you would get using NM in the first place.
SRT is essentially a 1:1 encryption of plain old Newtonian Mechanics (NM). SRT should be abandoned and replaced wherever it has been used, including in General Relativity Theory. As shown, Special Relativity Theory (SRT) is fatally flawed at its source.
The Interval Equation Shows the Error of Special Relativity Theory (SRT)
Dr. Sherwood Kaip
El Paso, TX
<skaip799@gmail.com>; cell: 1 (915) 309-6340
This material may be reproduced if author attribution is given.
To return from PRINT page, click "back" arrow on your browser