Site map of:

                  SRT Overview

     Encryption          NM from SRT

     SRT where why  E=mc2 flawed

        Interval              Rest Mass

        Algebra                E not saved

        SR < > NM            SRT vs. NM E

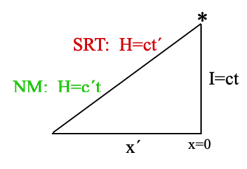
NM:   Vwrt x=0 = (x´/t) = (x´/I)c

SRT:   vwrt x=0=(x´/t´)=(x´/H)c

NM:   Vwrt* = (H/t) = (c´t)/t = c´

SRT:   vwrt * = (H/t´) = (ct´/t´) = c

     Consider just two quantities,  x´ ,  the distance an object has traveled, and  I , the distance a light flash has traveled during the same time  t  at speed  c .  We will assume that they both started out at  x=0.  Let’s play with these.  

Let   x´2 + I2 = H´2  ;      I2 = H´2 – x´2  ;      I2/t2 = H´2/t2 – x´2/t2

Let   x´>0;  I>0.  Therefore,   H´>I

γ2 = (ct´)2/I2= (H´/I)2 =H´2/(H´2–x´2)=1/1–(x´/H´)2

= 1/1–(x´/ct´)2 = 1/1–(v/c)2

γ = [1/(1–(v/c)2)]½ = (H´/I) = (ct´)/I

     The  γx  and  γ(v/c2)x of the full SRT transformation equations are readily derivable from the Relativistic Interval equation.

Simple Algebra and Special Relativity (SRT)

Dr. Sherwood Kaip

El Paso, TX

<skaip799@gmail.com>;   cell: 1 (915) 309-6340

This material may be reproduced if author attribution is given.

NM

Let        c=I/t;   c´=H´/t

Therefore,  

I=ct;   H´=c´t

Because  H´>I,  

c´ > c

NM     I2 = (c´t)2 – x´2

Let      V=x´/t

x´=(x´/t)t=Vt=(V/c)ct=(V/c)I

SRT

H´ > [ct = I]

Let   t´= H´/c

H´2 = (ct´)2

SRT     I2 = (ct´)2 – x´2

Let  γ=(H´/I)=(ct´/ct) [see below]

Let   v=(x´/t´)

x´=(ct´/ct)(x´/ct´)ct

=γ(v/c)ct=γvt

t´=(ct´/ct)t=γt

x´=Vt=γvt = γ(v/c)ct= γ(v/c)I

V=γv