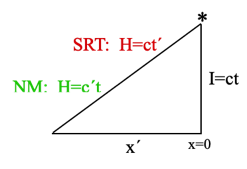Abstract
This derivation of the Newtonian Mechanics (NM) transform equation from the equations of Special Relativity Theory (SRT) uses no assumptions other than the ‘correctness’ of the SRT equations.
The derivation shows that SRT velocity, time, and distance do not necessarily correspond with those of NM. However there are equivalents for them between SRT and NM and these are shown.
The derivation of the NM transform equation from the equations of SRT results in a transformation equation that avoids ‘time dilation’, ’length contraction’, and does not involve the speed of light. NM and SRT are one to one mathematical transformations of each other as shown.
************
Assume the correctness of Special Relativity (SRT). and that light and other electromagnetic radiation will be measured to travel the same speed c in all reference frames. Therefore the following equations of SRT will be correct, and any equations mathematically derived from them are likewise correct. The transform equations of (SRT) are:
x' = γ(x + vt) = γ(v/c)ct + γx (1)
ct’ = γct + γ(v/c)x (2)
x = γ(x' –vt’) = –γ(v/c)ct’ + γx' (3)
ct = γct’ – γ(v/c)x' (4)
SRT Interval = I =((ct)2 – x2)1/2 =((ct’)2 – x'2)1/2 = , etc. (5)
(as defined in Taylor and Wheeler, “Spacetime Physics” and derivable directly from Eqs. 1 through 4). As Eq. 5 shows, the SRT Interval for any two events is the same in all reference frames. This Interval may henceforth be referred to as “I”.
γ (i.e., gamma) = (1 – (v2/c2))–(1/2), (6)
where v is the relativistic velocity between reference frames. x, t , and c are relativistic distance, time, and speed of electromagnetic radiation respectively.
By Eq. 5, the relativistic Interval=I=ct when x=0 ; also I=ct’ when x'=0 . Therefore,
x' = γ(v/c)I when x=0 by Eq. 1 and Eq. 5 (7)
ct’ = γt when x=0 by Eq. 2 and Eq. 5 (8)
x = –γ(v/c)I when x'=0 by Eq. 3 and Eq. 5 (9)
ct = γt’ when x'=0 by Eq. 4 and Eq. 5 (10)
Eq. 7 can also be written as
x' = γv(I/c) when x=0 (11)
and Eq. 9 can be written as
x = –γv(I/c) when x'=0 (12)
Since the Interval for two events is the same in all reference frames in SRT, we can henceforth refer to the (Interval/c) as “T” , using a capital letter to indicate that T is not frame specific. That is,
T = Interval/c = I/c (13)
Why use T (for time) rather than some other capital letter? If the square of the Interval, I2, as defined in
Eq. 5 is positive, the Interval is called “time-like” in SRT (although the Interval itself is a distance) because when two events occur a time apart, there is always some actual or potential reference frame which can move sufficiently fast that in that frame both events occur at the same place (delta x' or delta x equals zero). In that frame the two events are separated by only a time and not a distance. The relativistic (Interval/c) equals t ex'actly when delta x=0 ; the relativistic (Interval/c) equals t’ ex'actly when delta x'=0 . Since, by SRT, the Interval is the same in all reference frames for any two specific events, the Interval/c is therefore that time. All instances of one object moving relative to another fit into this category of a “time-like” Interval. (If two objects are not moving with respect to each other, then the Interval in that frame is “space-like”—the square of the Interval is negative—and is of course the same “space-like” Interval in all other reference frames moving with respect to that frame.)
So now we can write
x' = γv(I/c) = (γv)T when x=0 and (14)
x = –γv(I/c) = –(γv)T when x'=0 (15)
This means that ACCORDING TO SRT the distance one point [i.e., x=0 or x'=0 ] of any reference frame [e.g., call it frame A] travels through any other reference frame [call it frame B] moving with respect to the first [frame A] is (γv)T where T is the Interval/c and this Interval is the same in all reference frames for any two particular events. One point [of frame A] moves the distance (γv)T [through frame B] and the other point [of
frame B] moves in the opposite direction the distance MINUS (γv)T [through frame A]. Since the Interval/c is the time (no distance involved) according to SRT that one point of a frame moved through another frame, then it is reasonable to say that
x'/T = γv = V (for the point x=0 from Eq. 11) (16)
–x/T = γv = V (for the point x'=0 from Eq. 12) (17)
where V is a velocity which shows how far an object [point of one reference frame, x=0 or x'=0 ] has traveled through another reference frame during the time T which according to SRT is the same in all reference frames for any two particular events. This is what we mean by velocity—the distance traveled by a point of one frame through another divided by the time of that travel. This equals
V = γv (18)
Thus we now can express an SRT time which is the same in all reference frames and a velocity,
V =γv , which enables us to state that the distance an object [one point] travels through another reference frame is
V T and the distance an object [one point] at rest in the latter frame travels through the first is – V T. Notice that if T is held constant the distance moved by the point of frame A through frame B is the SAME as the distance moved by the point of frame B through frame A (but in the opposite direction, of course). And this is ALL according to SRT.
Compare this with using t' , t , v , and γ in SRT where for x=0
x' = γ(vt + x) or (1)
x' = γvt + 0 or
x'=γvt (19)
but for the same time t , x'=0 falls in the unprimed frame at
x' = γ(vt + x) = γ(v/c)ct + γx or (1)
0 = γvt + γx or
x = –(γvt)/γ (20)
meaning that at time t , x=0 moved the distance γvt through the prime frame while x'=0 is at only the distance (1/γ) times that distance in the unprimed frame in the opposite direction. This is because the Interval is no longer the same. Obviously Eqs. 14 and 15 are much simpler to visualize for points [ x’=0 or x=0 ] moving through each other’s reference frame than Eqs. 19 and 20, even though both methods are according to SRT.
Eq. 7 and Eq. 9 are fine for when x=0 and x'=0 , respectively, but what if both those values are not zero? These transform equations are incomplete. We must have equations that cover the situation where both distance values are non-zero. We need to find what function of x and x' respectively need to be added to make the equations correct for values of x and x' respectively not equal to zero.
When x=0 ,
x' = γ(v/c)I (7)
So the value of x' when x≠0 is the value of x' when x=0 plus an additional amount, an unknown function
of x , which we will label f(x) . Rewrite Eq. 7 as
x' = γ(v/c)I + f(x) (21)
Likewise, when x'=0 ,
x = –γ(v/c)I (9)
and the value of x when x'≠0 is the value of x when x'=0 plus an additional amount, an unknown function
of x' , which we will label h(x') . Rewrite Eq. 9 as
x = –γ(v/c)I + h(x') (22)
Our job here is to find the value of the functions f(x) and h(x') . Using Eqs. 21 and 22, we find that
x' – f(x) = γ(v/c)I = h(x') - x (23)
or
x' - f(x) = h(x') - x (24)
f(x) is a function only of x and h(x') is a function only of x' . Setting x=0 , f(x)=0 and
h(x')=x' (25)
Setting x'=0 , h(x')=0 and
f(x)=x (26)
and thus the full **SRT** Eqs. 21. and 22. become
x' = γ(v/c)I + x and (27)
x = –γ(v/c)I + x' (28)
Of course, Eqs. 27 and 28 are the same! So substituting for (γv) and (I/c) , Eqs. 18 & 13, we now have
x' = V T + x or X’ = V T + X (29)
where T is as derived for Eq. 13.
This of course is the same as the Gallilean Transform equation of Newtonian Mechanics (NM)!!! However, I have derived it only and directly from the equations of SRT. Eq. 29 is true at all values of V =γv , Eq. 18, not just at slow speeds. It applies to all objects moving with respect to each other. V , V/c , and γ(v/c) can approach infinity, in which case, v , the usual ‘velocity’ of SRT, is approaching 1.0c .
Eq. 29 says nothing about light. V is simply the ratio of distance traveled through a reference frame by a point of another frame during the frame-independent SRT (Interval/c)=T (Eq. 13) which, by definition is the time on a clock not moving in its reference frame (i.e., delta(X)=0 or delta(X’)=0) . V therefore has nothing to do with the speed of light. (I/c)=(ct)/c=t when delta(X)=0 and (I/c)=(ct')/c=t' when delta(X’)=0 .
Notice also that if T=0 , X=X’ . There is no length ‘contraction’. X is the sum of how far the origin X’=0 traveled from X=0 during the frame independent time function I/c=T , plus the value of X’ . For a given value of V T , changes in X equal exactly changes in X’ and these changes in X caused by changes in X’ are not affected by speed. (In contrast, when t or t are used instead of T , offsets in x or x' affect x' or x by the factor γ where γ is a function of speed. See Eq. 1 and Eq. 3.)
SUMMARY
All of this has been about objects (and the reference frames in which they are each ‘at rest’) moving relative to each other, which means that a point of one reference frame changes location in the other frame linearly with succeeding time. In SRT this time is usually characterized by different values in the two reference frames ( t' and t ) but I have shown that this time can be characterized, according to the rules of SRT, as a single value for time in all reference frames, namely the SRT (I/c)=T which is the same in all reference frames for any two given events. This is the same as the time on a non-moving clock read in its reference frame. It is also the time of everyday Newtonian Mechanics (NM) and in SRT is called ‘proper time’. Furthermore, the ratio of the distance one point moves through the other frame to this frame-independent T=(I/c) is what we normally mean by velocity and equals V =γv where γ is the “gamma” of SRT defined in Eq. 6 and v is what is usually called velocity in SRT. Since γ (gamma) is dimensionless, γv is equally valid to use as a velocity and this γv= V is the velocity of NM.
Thus Eq. 29, derived directly and only from SRT, shows that the equations of NM are just as good as the usual ones of SRT (in fact better and simpler) to describe the relationship of objects moving with respect to each other even at ex'treme speeds if we recognize that the NM time T in Eq. 29 equals
[((ct)2 – x2)1/2]/c = [((ct')2 – x'2)1/2]/c = (I/c) = T
and that the NM speed V in Eq. 18 equals γv where v is the relativistic ‘velocity’ of SRT.
RECAP
Look at the Equations 1 through 6 of SRT. I won’t repeat them here.
7. x' = γ(v/c)Interval when x=0
9. x = –γ(v/c)Interval when x'=0
Define NM time T , constant in all reference frames, in terms of the SRT Interval:
13. T = Interval/c
Define V , the velocity of NM, in terms of SRT ‘velocity’ v :
16. x'/T = γv = V (for the point x=0 from Eqs. 7, 13, and 18)
17. –x/T = γv = V (for the point x'=0 from the Eqs. 9, 13, and 18)
Therefore
14. x' = γv(I/c) = V T when x=0 and
15. x = –γv(I/c) = – V T when x'=0
Eqs. 14 and 15 (and 7 and 9) are fine when x=0 or x'=0 but what if neither is zero? We must find f(X) and h(X’) in the following equations:
21. X’ = γ(v/c)Interval + f(X) = V T + f(X) from Eq. 7
22. X = –γ(v/c)Interval + h(X’) = – V T + h(X’) from Eq. 9
Set X=0
X’ = γ(v/c)Interval + 0 = V T + 0
0 = – γ(v/c)Interval + h(X’) = – V T + h(X’)
Adding,
25. h(X’) = X’
Set X’=0
0 = γ(v/c)Interval + f(X) = V T + f(X)
X = –γ(v/c)Interval + 0 = – V T + 0
Again adding,
26. f(X) = X
Both Equations 21 and 22 then become
29. X’ = V T + X
the Gallilean transform equation of NM, derived from SRT.