Site map of:
E = γmc2
I2 = (ct)2 – x2 = (ct´)2 – x´2 =…
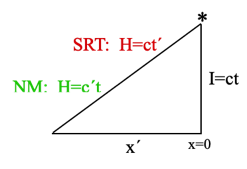
NM: Vwrt x=0 = (x´/t) = (x´/I)c
SRT: vwrt x=0=(x´/t´)=(x´/H)c
NM: Vwrt* = (H/t) = (c´t)/t = c´
SRT: vwrt * = (H/t´) = (ct´/t´) = c
Special Relativity (SRT) and Newtonian Mechanics (NM) are about distances (locations), time, and ratios between these, called velocities. An object having mass m or a reference frame changes position with respect to a moving light pulse during a time period t . Consider the reference frame of the light source as non-moving and the object as moving with respect to that light source.
Let us say that a light starts vertically from its source just as an object is passing by horizontally. Because the motions are perpendicular, this physical situation can be described by the Interval equation
x´2 + (ct)2 = x´2 + I2 = H2
where x´ is the distance the object has moved horizontally while the light ray has moved vertically the distance I during the time t at the speed of light, c . H2 is the sum of those squares.
c = I/t ; I = ct ; t=I/c
The velocity of the object relative to the light source is V = x´/t = (x´/I)c . The speed of the vertically traveling light relative to the object is the distance H divided by t which result is obviously greater than c since H>I . Let us call it c´ . So for NM,
H2 = x´2 + I2 ; H = c´t .
However, this is not acceptable to Einstein’s Second postulate presumption that light travels the same speed relative to everything, i.e., relative both to its source and to the horizontally moving object. Therefore, in SRT, in order to keep c constant, SRT says H = ct´ . This gets around the problem of having to admit that the light is traveling at a greater speed, H/t , relative to the object than (I/t) = c , the light relative to its source.
The actual SRT Interval equation, which is the basis of all the equations and concepts of SRT, is
I2 = (ct)2 – x2 = (ct´)2 – x´2 = (ct´´)2 – x´´2 …
which in slightly different form is
x´2 + I2 = H2 = (ct´)2
compared with the NM Interval equation
x´2 + I2 = H2 = (c´t)2
Note that H2 = (ct´)2 = (c´t)2 has the same numeric value in both NM and SRT.
Also note that both the NM and the SRT depictions are describing the exact same physical situation. This portrayal is a generalized representation which covers any movement of anything over time, compared with light. Therefore, either NM or SRT could be used to describe movement relative to light speed but SRT makes a mockery of speed and time to claim that something, the moving light front, can go the same speed with respect to two things, the light source and the object, which are moving with respect to each other (Einstein’s Second postulate).
Because the physical situation is the same in both systems, NM and SRT are 1:1 mathematical transformations of each other, i.e., if you know the NM depiction, you can create the SRT depiction, and vice versa. Let us now do that.
NM<———>SR
The NM transformation formula is
x´ = Vt + x = (V/c)ct + x = (V/c)I + x
while the SRT transformation formulas are
x´ = γ(vt + x) = γ(v/c)ct + γx
t´ = γ(t + (v/c2)x) ; ct´ = γct + γ(v/c)x
where γ (gamma) is the well-known SRT expression γ = 1 / (1 – (v/c)2)½ .
Gamma also has several other useful definitions easily derived from γ 2 .
γ2 = [1 / (1 – (v/c)2)] = [1 / (1 – (x´/ct´)2)] = [(ct´)2 / ((ct´)2 – x´2)] = [(ct´)2 / (ct)2] = H2/I2
γ2 = ((ct´)2 / (ct)2) = (x´2 + (ct)2) / (ct)2 = (x´2 / (ct)2) + ((ct)2 / (ct)2) = ((V/c)2 + 1)
γ2 = ((ct´2 / ct2)) = (x´2/(ct)2) (ct´2/x´2) = (V/c)2 / (v/c)2 = V2 / v2
Thus, γ = H/I = ((V/c)2 + 1)1/2 = (V/v) = (V/c) / (v/c) = (ct´) / (ct) as well as
1 / (1 – (v/c)2)½ .
In converting from the NM depiction of two events to the SRT depiction, or vice versa, it is necessary to distinguish between the NM and SRT form of some variables because they use the same labels but have different values in the two systems. The SRT Interval equation, valid for all reference frame views of two given events, is
I2 = (ct)2 – x2 = (ct´)2 – x´2 = (ct´´)2 – x´´2= …
This requires that the ctR of relativity be (ct)R = (I2 + x2)½ rather than the (ct)N=I of NM. It also requires differentiating between the final x primes (x´N and x´R), the location of the x point of the non-moving reference frame in the object’s moving reference frame after the time t . Taking this into account, the transformation equations are:
NM: x´N = VtN + x = (V/c)(ct)N + x = (V/c)I + x
SRT: x´R= γ(v/c)(ct)R + γx = γ(v/c)(I2 + x2)1/2 + γx
ct´R = γctR + γ(v/c)x = γ(I2+ x2)1/2 + γ(v/c)x ; t´R = γ(tR + (v/c2)x) .
The x is the same in both NM and SRT. Note that ct´R and ctR are not the same. They refer to different reference frames; in this case, the moving and non-moving reference frames, respectively. The SRT Interval equation, which is the real heart of SRT, requires that the SRT Interval I be the same in all reference frames. This means that, when x≠0 , the ctR of SRT must be greater than the ctN=I of NM so that ctR equals (I2+x2)1/2 to keep the SRT Interval equation valid and equal to I in all cases, i.e., ctR2 – x2 = (I2+x2) – x2 = I2 .
NM to SRT
To convert the NM depiction to the SRT depiction, first finish the NM equation so that you have all the NM values. Then, replace the SRT values on the left of the = sign below with the NM values on the right of the = sign. The x of SRT equals the x of NM and
γ =((V/c)2 + 1)1/2 ; (v/c)=(V/c)/γ ; I=ctN ; ctR = ((ctN)2+ x2)1/2 = (I2+ x2)1/2 .
Now calculate x´R and t´R using the SRT transformation equations. If (ct´R)2 – x´R2 = I2 , you have probably done the problem correctly.
If x=0, as is usually the case, then the conversion is simply: γ(v/c)=(V/c) , ctR=ctN=I , ct´R=γct , and x´R=x´N . Note that V=γv and, when x = 0 ,
(V/c)I = (V/c)(ctN) = x´N = x´R= γ(v/c)(ctN) = γ(v/c)I
SRT to NM
To convert the SRT depiction to the equivalent accurate NM depiction, complete all the values for the SRT depiction. Then, the NM values are derived from the SRT values as follows:
(V/c) = γ(v/c) , xN = xR , ctN = I = ((ct´R)2 – (x´R)2)1/2 = ((ctR)2 – (xR)2)1/2 .
Note that ct´R ≠ ctR .
Example 1
Something travels 400 meters in 1.0 microsecond. Find the NM values.
x´N = VtN + x = (V/c)ctN + x = (V/c)I + x
x´N = 400m ; tN = 1.0µsec ; x = 0 ; V = 400m/µsec ; (V/c) = 4/3 ; I=300m
Notice that the object traveled 400m while light travels only 300 m in 1.0µsec. But this is OK in SRT as shown next in the SRT version of the exact same physical situation just described.
Find the SRT values, realizing that ((ct)R2 – x2)1/2 must equal I , i.e., (ct)R = (I2 + x2)1/2 .
x´R = γ(v/c)(ct)R + γx = γ(v/c)(I2+ x2)1/2 + γx
x´R = 400m ; tR = 1.0µsec ; x = 0 ; (ct)R = (3002 + 02)1/2 = 300m = I ;
γ = ((4/3)2 + 1)1/2 = 5/3 ; (v/c) = (V/c)/γ = (4/3)/(5/3) = 0.8 ; [γv=V]
ct´R = γctR + γ(v/c)x = γ(I2+ x2)1/2 + γ(v/c)x ; t´R = γ(tR + (v/c2)x)
ct´R = (5/3)(300m) + 0 = 500m ; t´R = (5/3)µsec
Example 2
A very fast train passes the station at 0.8 times the speed of light, v/c=0.8 . After t = 1.0µsec , a light emitted from the station as the front of the locomotive passed by has traveled 300m [1.0µsec]. Where is a point 200m back from the station located in the train’s reference frame?
given: (v/c)=0.8 ; I = ct = 300m ; x = 200m
SRT: x´R = γ(v/c)(ct)R + γx = γ(v/c)(I2+ x2)1/2 + γx
γ = 1/(1 – 0.82)1/2 = 5/3 ; (ct)R = (3002 + 2002)½ = 360.555 ;
x´R = (5/3)(4/5) 360.555 + (5/3) 200 = 814.0733…m (greater than 200m beyond the 400m where the station would be in the moving train’s reference frame).
ct´R = γctR + γ(v/c)x = γ(I2+ x2)1/2 + γ(v/c)x ; t´R = γ(tR + (v/c2)x)
ct´R = (5/3) 360.555 + (5/3)(4/5) 200 = 867.5919m
I2 = ct´R2 – x´R2 = (867.59192 – 814.0 7332) = (ct)R2 – x2 = 360.5552 – 2002 = 90,000
I = 300m
Converting this same problem from SRT to NM:
(V/c) = γ(v/c) = (5/3)(4/5) = (4/3) ; x = 200m ; ct = I = ((ct´R)2 – (x´R)2)½ = 300m
x´ = Vt + x = (V/c)ct + x = (4/3) 300m + 200m = 600m
just as you would expect if you had done the problem in NM in the first place.
Conclusion
Both Special Relativity theory (SRT) and Newtonian Mechanics (NM) can be derived from a generalization of the SRT Interval equation: x´2 + I2 = H2 in which I is the distance a light beam has traveled at the speed of light c for the time t , x´ is the distance an object has traveled from the light source perpendicularly to that light beam during the time t , and H is the distance between the location of the object and the light beam after time t . Since H>I , the velocity of the light beam (or anything else) relative to the object, H/t , is greater than the velocity of the light beam relative to its source I/t . Einstein’s Second Postulate promulgates that the speed of light is the same in all reference frames. Accordingly, the obvious NM view that (H/t ) > ((I/t) = c) is changed to H = ct´ in order to keep c the same in both equations.
Thereafter, t´ is the ‘time’ used in SRT for computing the velocity of the object’s moving reference frame, resulting in
(x´/t´) = (x´/(H/c)) = (x´/H)c = (x´ / (x´2 + I2)1/2)c .
This explains why the velocity in SRT (x´/t´) = v is always less than c , versus the V = (x´/t) of NM.
It is shown that any physical situation can be described by either an NM or an SRT depiction and further that there is a 1:1 mathematical relationship between the NM and SRT depictions. The article describes exactly how to transform the equations of the NM depiction into the SRT depiction and vice versa. Since the depictions are nterchangeable, the NM description gives the usual meaning of speed without creating a pseudo mathematical ‘time dilation’ and avoids the SRT paradoxes such as the the twin paradox and the barn/pole paradox.
SRT to NM and vice versa
Dr. Sherwood Kaip
El Paso, TX
<skaip799@gmail.com>; cell: 1 (915) 309-6340
This material may be reproduced if author attribution is given.
To return from PRINT page, click "back" arrow on your browser