Special Relativity

        SR Begin       

        E=mc2 –not

        SR End

         SR Model

         NM from SR

         Enegy & Mass

        NM SR diagram

         SR Time

         SR Rest Mass

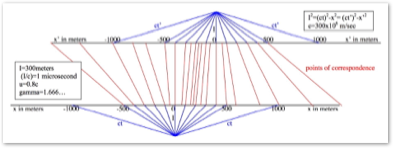
     The three equations below are all simultaneously true according to Special Relativity.  The first equation implies that mass increases with energy and this is what Einstein believed in his article, “Does the Inertia of a Body Depend on its Energy Content?”.  Recent physics seems to try to ignore this “relativistic mass”  m   and concentrate on Relativistic energy and momentum.

E = mc2

E0 = m0c2

E2 = (Pc)2 + (m0c2)2

     In the same sense, the kinetic energy of Newtonian Mechanics could be said to be  E=½ m ,  in which case the  ´m´  mass would change with changes in kinetic energy.  Of course this  ´m´ equals  m0v2 .  Likewise, the  ´m´  in  E=mc2  should read:   E equals gamma times  m0c2 .  There is no  ´m´  which varies with  E ; only  m0,  which is constant, and gamma, which causes the changes in  E .  The  u is the Relativistic velocity, always less than  c ,  the speed of light.  The proof follows:

E2 = (m0γuc)2 + (m0c2)2

[E2 / (m0c2)2)] = [(m0γuc)2 + (m0c2)2)] / (m0c2)2

[E2 / (m0c2)2)] = γ2(u/c)2 + 1

γ2 = 1 / [1–(u/c)2]

[E2 / (m0c2)2)] = {(u/c)2 / [1–(u/c)2]} + {[1–(u/c)2] / [1–(u/c)2]}

[E2 / (m0c2)2)] = [(u/c)2 + 1 – (u/c)2] / [1–(u/c)2]

[E2 / (m0c2)2)] = [1 / 1 – (u/c)2] = γ2

E = γmc2

This precise equation resolves the confusion of Relativistic  ´m´ ;

mass does not change due to velocity change [relative to ?]!

SRT reveals  E = mc2  is flawed

Dr. Sherwood Kaip

1305 Cessna Dr.; El Paso, TX 79925

This material may be reproduced if author attribution is given.