1. Introduction
Consider an object (Obj1) that can be defined as 'not moving'. Let it send out timing signals from itself, in all directions, at a known speed s . Consider the portion of the timing signal that is going in one direction; call it the ' y' direction. Hereafter, this direction will be called 'vertical', The signal can be considered a timing signal because its speed has been measured many times in Obj1's reference frame, and s is always the result.
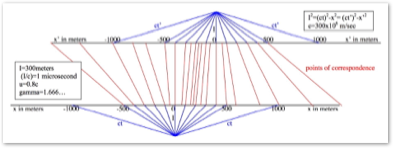
A second object (Obj2) is moving by in a perpendicular direction, which will hereafter be called ´horizontal’. When the moving Obj2 passes the non-moving Obj1, time t=0 , the Obj1 sends out its timing signal vertically (as well as spherically) at speed s . At a later time t , the timing signal has traveled during the interval t the vertical distance I=st . In the meantime, Obj2 has traveled horizontally the distance x . The velocity of Obj2 with respect to Obj1, is:
V = x´/t = x´/(I/s) = (x´ I)s ; (1)
i.e., the ratio of the distance that Obj2 traveled, x´ , to the distance the signal traveled, I , times the timing signal speed s .
2. Analysis
During the time t , the objects have moved the distance x´ horizontally from each other, and the timing signal has moved the distance I vertically from Obj1. So during the time t , the timing signal has moved the combined vertical and horizontal distance H along a diagonal path relative to Obj2:
__________
H = √(x´)2 + I2 . (2)
The ratio H/t can be called s´ , and understood as the speed of the timing signal in the reference frame of Obj2, So H = s´t . Obviously, s´ is greater than s . We can re-write the previous formula as
I2 = H2 – (x´)2 = (s´t)2 – (x´)2 . (3)
I can be called the 'Interval' because it is the distance the timing signal has traveled in its own (i.e., Obj1’s) reference frame.
Note that if Obj2 had traveled at a different speed V´´ for the different distance x” , then I would still be the same, and would still represent the time t , since the timing signal always travels at speed s from Obj1 .
A term I has been defined, although there would seem to be little use for it in Newtonian Mechanics (NM). Another variable can be defined: as ‘gamma' (γ) :
γ = H/I = s´t/I = s´t/st . (4)
This γ is tire ratio of the distance H that the timing signal traveled in the frame of the moving Obj2 to the distance I that the timing signal traveled in its own non–moving frame.
Later, γ will be shown in another form that is probably more familiar. It will still be the ratio of these two distances.
This has all been straightforward, though unusual, Newtonian Mechanics (NM). But let us now change something. Suppose we insist (propose, postulate, etc.) that Obj1's timing signal travels at the same speed in both Obj1's and Obj2's reference frames. If you think about it a bit, this is physically impossible. Nothing (including the timing signal) moving away from its source can possibly move the same speed with respect to an object moving toward or away from the source. A man running forward on a moving train is not running the same speed with respect to the ground as he is moving with respect to the train. Not if we consider what we normally mean by distance, time, and velocity! A flag being raised at 4 m/s vertically on a train moving 3 m/s is moving up and forward at 5 m/s with respect to the ground, not 3 m/s . But let's proceed anyway.
In other words, s´ = s , or H /t = I/t , which means I = st and also H = st , or I = st = H , which is obviously not the case. But if we let I = st and H = st´ , then H > I is no problem. We have:
I2 =H2 – (x´)2 = (st´)2 – (x´)2. (5)
Then γ is still
γ = H/I = st´/I = st´/st . (6)
If we put the Interval Equation in the form of a triangle where the vertical leg is the distance I that the timing signal traveled at speed s for time t , the horizontal leg is the distance x´ that Obj2 traveled from Obj1 during the time t , and the hypotenuse is H = st´ , the distance the timing signal traveled in Obj2's reference frame, what preceded and what follows may become clearer.
Although we solved one problem, that H ≠ I , we created a new problem: deciding which 'time' to use for calculating the speed of the moving object relative to the non-moving object. Since the 'prime' moving Obj2's reference frame seems to have a new time, we define a different velocity between Obj1 and Obj2:
v´ = x´/t´ , v´/s = x´/st´ = x´/H. (7)
Eq (6) defined: γ = H /I = s´t/st = st´/st . Squaring yields:
γ2 = H2/I2 = (st´)2 / [(st´)2 – (x´)2 ]. (8)
Dividing numerator and denominator by (st´)2 yields:
γ2 = H2 /12 = 1/[1 – (x´2 / (st´)2l = 1/[1 – (v´/s)2] .
and __________
γ = 1 /√ 1 – (v´/s)2 . (10)
If c is substituted for s , this is the usual way γ is written in Einstein's SRT. We now have enough information to determine quantities in the moving frame from quantities in the non-moving frame. In terms of t ,
x´ = (st´/st)(x´/t´)t = γvt = γ(v/s)st , (11)
t´ = (st´/st)t = γt and st´ = γst . (12)
The full transformation equations in SRT are:
x´ = γ(x + vt) = γx + γvt = γ(v/c)ct + γx , (13)
t´ = γ(t + vx/c2) or ct´ = γct + γ(v/c)x , (14)
where c replaces s , as explained below. These are the same as the ’s’ equations, except for the added term in each. There are two more SRT transformation equations, for values of x and t in terms of x´ and t´ , which can be derived after manipulating these.
If we change all of the above s's into c's, we get the equations (and concepts) of Einstein's SRT derived by turning the NM form of the Interval equation into the SRT Interval equation. Obviously, H is greater than I , and therefore the speed of the timing signal in the reference frame of Obj2, s´ , is greater than the speed s of the timing signal in the reference frame of Obj1 because of the added horizontal component. However, by 'postulating' that the velocity of the timing signal is the same in both frames and compensating for the fact that H > I by making a 'new' time, t´ , greater in the moving reference frame of Obj2, Einstein's SRT has just been created. This is the exact point where NM becomes SRT.
The full SRT transformation equations add γx for the first one and γ(v/c2)x for the second one. These two equations in terms of s and the other two (reverse) transformation equations, derivable from the above, can be used to derive the terms γx and the γ(v!c2) needed to complete the SRT transformation equations. This will not be shown here, but can be seen on-line in Sect. 5.5 of the article titled "A simple Special Relativity model is offered which easily explains the 'twin paradox', why c is a maximum speed limit, and makes the concepts of SRT easy to understand," available in the Special Relativity section of the website www.trybasics.com and also referred to as "SR Model". Accessed 4/11/19.
The important thing to note here is that the SRT equations were based, not on the speed of light, but only on a timing signal of some known speed s . The speed s is totally arbitrary. It doesn't have to be the speed of light, usually written c . The equations in terms of s are exactly the same as the SRT equations in terms of c . This demonstrates that SRT is about Mathematics, not about Physics. Note also that there was only one physical situation described, and it was described correctly for both NM and SRT. This demonstrates that there is a 1:1 mathematical correspondence between NM and SRT.
From either the s equations above, or the same actual c equations of SRT, it can be seen why, according to SRT, nothing can go faster than light speed c . The SRT velocity is:
________
v´/c = x´/ct´ = x´/√ (x´)2+I2 . (15)
Obviously, this will always be < 1.0 . On the other hand, the NM velocity V/c = x´/ct . The distance that Obj2 has moved past Obj1 is:
x´ = Vt = (ct´/ct)(x´/t´)t = γvt . (16)
When working from one point in the non-moving reference frame (x=0) , to convert from SRT to NM, or vice versa
V = γv , v = V/γ , (17)
γ = H/I = (ct´)/I (SRT) = (c´t)/I (NM), (18)
but has the same numerical value in both; i.e.,
γ2=1 / [l–v2/c2] = l + (V2/c2) . (19)
and t´ = γt , t = t´/γ = I/c (20),(21)
SRT time t´ is a function of NM time, velocity, and location}, equals (NM) time equals (SRT) 'proper time'.
I2 =[(ct´)2 – x´)2] (SRT) , [(c´t)2 – (x´)2] (NM) , (22)
but has the same numerical value in both, and ct´ = c´t . The speed of the timing signal, s or c , is not needed in NM unless velocity is being expressed as V!c . The timing signal serves only to provide the time, which is the same in all reference frames (like I/c in SRT).
Either NM or SRT can be used to solve problems involving time/distance/velocity; however, NM does not mess with concepts of time and distance. Since any SRT problem can also be accurately described in NM, there really is no time dilation, or consequent length contraction.
Objects can go at any speed faster than light, and according to (SRT), as shown by
x´/I = γ(v/c) . (23)
Because of γ , the distance x´ traveled by Obj2 from Obj1 approaches infinity as v/c approaches 1.0 . Of course, v/c will always be < 1.0 for moving objects..
In NM, momentum is P = mV, and in SRT, P = mγv, but since V= γv, the value for momentum P is the same in both.
Since collision problems can be solved using only momentum P and mass m , collision problems can be solved without invoking SRT because P = mγv = mV .
Multiplying the Interval equation I2 = (ct´)2 – (x´)2 by various values is the easiest way to get some of the other formulas used in (SRT). Without further explanation, here are some examples that the author has derived in this way:
(γmc2)2 – (mc2)2 = Pc)2 , E2 – (E0)2 = (Pc)2 , (24,25)
E0=mc2 , E = γmc2 , γ2 – 1 = (V/c)2 = [γ(v/c)]2 . (26,27)
3. Conclusion
The famous Einstein equation E = me2 is incorrect— the actual correct (SRT) equation is E = γmc2 . The mass itself (often called 'rest mass', and distinguished as m0) is a constant that does not vary with velocity or kinetic energy—only γ varies. This does not mean that mass and energy cannot interchange — just not due to velocity or kinetic energy per se.
Note also that E0 is due to mass m , and therefore E is merely a stand-in for momentum P , and γ is a stand-in for the NM value V/c ; or, if you prefer, for the γ(v/c) of SRT.
What has been shown here is that SRT is derivable from NM in a way that reveals how SRT is always convertible into NM with total accuracy, and vice versa. However, since this SRT math derives from a physically impossible premise, it is silly to use it. The SRT math, not reality, is what creates time dilation, maximum velocity limit of c , and light rays in every direction traveling the same speed with respect to everything in the universe moving in every direction with various velocities.
By the way, there are other ways to show that (SRT) is just plain not possibly correct, even though time/distance/velocity and collision problems can be worked, thanks to its relationship to Newtonian Mechanics (NM). To again show this 1:1 relationship between SRT and NM, go to the article titled "How to derive Newtonian Mechanics Directly from Only the Equations of Special Relativity", available in the Special Relativity section of the website www.trybasics.com and also referred to as "NM from SR". Accessed 4/11/19.
To return from PRINT page, click "back" arrow on your browser
The Beginning of Special Relativity Theory
Published in Galilean Electrodynamics May/June 2020; Vol. 31 No.3
Dr. Sherwood Kaip
email <skaip799@gmail.com>; cell (915) 309-634