Using only the Interval Equation (IE) from Special Relativity Theory (SRT), and that from Newtonian Mechanics (NM), the coordinate transformations of SRT and of NM are derived, and shown to be convertible into each other. This exercise invalidates the current idea that SRT is correct, while NM is in error, although adequate at speeds small in comparison to the speed of light, c . How these results affect the ideas of time dilation and c as a speed limit is discussed. Reference is also made to Einstein’s interpretation that changes in kinetic energy result in changes in ´mass´. This does not preclude that energy can be turned into mass and vice versa; it means only that kinetic energy changes need not be interpreted as mass changes.
1. Introduction
Einstein created his Special Relativity Theory (SRT) from his then new Second Postulate: "Light is always propagated in empty space with a definite velocity c which is independent of the state of motion of the emitting body." This gave an explanation for the null result of the Michelson-Morley experiment, for which there was no other acceptable explanation at the time. And at low speeds, it gave almost the same results as Newtonian Mechanics (NM). So it became accepted, including its odd concepts, such as time dilation, length contraction, and its speed limit c , the speed of light. But, we ask, speed relative to what? Apparently, everything! This does not comport with our usual understanding that everything will have different speeds relative to different objects moving in various ways. The present paper examines the situation using only the Interval Equations (IE´s) of SRT and NM and the transformation equations of SRT and NM. Important conclusions emerge from this examination.
2. The Examination
2.1 The Physical Situation
In a given reference frame, an omni-directional light starts out from x=0 at speed c for time t . The distance the light traveled, defined as I , is ct . Beginning at the same time, an object moves in the x direction from the location x=0 at Newtonian velocity V for a distance x´ during the same time t=I/c . (Any inertial movement situation can be converted to movement only in the x direction by rotating the coordinates as necessary.)
2.2 The Equivalent Interval Equation of NM
Let a prime (´ ) indicate a variable value in the reference frame considered to be moving. We have two distances, x´ , the distance the object moved relative to the non-moving, un-primed frame origin x=0 , and I=ct , the distance the light moved from x=0 in the non-moving unprimed frame. This x´ and I is all the information needed to determine the Newtonian velocity V of x´ away from x=0 :
V = x´/t = x´/(I/c) = (x´/I)c . (1)
We can form the quantity
(H´)2 = (x´)2 + I2 . (2)
Eq. (2) is the Interval Equation of NM. It will shortly be shown to have the same value as the SRT Interval. As can be seen from Eq. (2), this is a vector addition of the distance x´ that the object traveled through the non-moving reference frame and the distance I that the perpendicular portion of the spherical light traveled in the non-moving frame. The x´ is the distance the x=0 of the non-moving un-prime is away from the x´=0 point of the moving frame. Then H´ is the distance between where the object is at x´=0 and where the perpendicular portion of the spherical light front is after time t ; i.e., distance I=ct from x=0 perpendicular to the x direction.
From our viewpoint, the object traveled at speed V=x´/t to reach its current location. Meanwhile, the light traveled at speed
c = I/t . (3)
However, from the object’s viewpoint, the light traveled the distance H´ during the time t at speed:
c´ = H´/t . (4)
This speed c´ from (4) in the object’s moving reference frame is greater than c=I/t from (3) in the light’s non-moving reference frame. From (4),
H´ = c´t . (5)
Therefore, the NM Interval Eq. (2) can be written
(x´ )2 + I2 =(c´t)2 . (6)
To cover other objects at the same time but moving different x distances starting from x = 0 , we can say:
I2 = (ct)2 – x2 = (c´t)2 – (x´)2 = (c´´t)2 – x´´)2 = (c´´´t)2 – (x´´´)2… (7)
Here I is the distance the light has moved in the non-moving reference frame.
Understanding the Interval Equations of NM and SRT is critical to understanding the nature of SRT and its similarities and differences with NM.
2.3 The SRT Interval Equation
Using the same physical situation of a moving object, light in non-moving reference frame, and the meaning of c , x´ , I , and t=I/c , the SRT depiction is this. Adding distances x´ and I like perpendicular vectors, one gets the exact same Eq. (2).
However, there is a problem. By Eq. (3), the light moved at speed c perpendicularly in the non-moving reference frame, but by Eq. (4) the light moved at the greater speed c´ = H´/t (relative to the object now the distance x´ away) in the reference frame of the moving object.
In SRT, this is not allowed. By Einstein's Second Postulate, light can travel only at speed c in any reference frame. Since, according to SRT, c must always be the same, and
H´ ≠ ct , (8)
this is accomplished by changing the value of H´ to
H´ = ct´ . (9)
That is, since the value by Eq. (2) is 'correct' by definition, the only way to limit the speed of light to c in the moving reference frame is to change H´ to Eq. (9).
This is the creation of SRT, and its 'time dilation'. The effect is not physical, but rather the perverse result of a Postulate that insists that something, light or anything else, moves at the same speed in both of two different reference frames that are moving with respect to each other. If you think about this, this is a physical impossibility – if by 'speed' you mean distance traveled during one time unit. The distance H´ is obviously greater than the distance I . But let us continue with the SRT mathematics.
Eq. (2) can be re-written as:
I2 = (H´)2 – (x´)2 . (10)
Eq. (10) is true for both SRT and NM, and the numerical value of H´ is the same for both. However, in NM, H´=c´t [Eq. (5)], but in SRT, H´=ct´ [Eq. (9)]. This is the exact point where NM changes to SRT, i.e., changing Eq. (5) to Eq. (9). So for SRT, Eq. (10) then becomes:
I2 = (ct´)2 – (x´)2 , (11)
so, extending to indefinitely more frames,
I2 = (ct)2 – x2 = (ct´)2 – (x´)2 = (ct´´)2 – (x´´)2 +… . (12)
This is the usual form of the SRT Interval Equation. The I is constant in all reference frames. Note that the (ct)’s depend, not only on the time the light traveled the distance I at speed c , but also on the various x’s . And of course the NM Interval Equation, Eq. (7), can be put in the equivalent forms:
I2 = (ct)2 –x2= (c´t)2 –x´2 = (c´´t)2 –x´´2… . (7a)
2.4 Velocity in NM and SRT
In SRT, the velocity of the moving object with respect to the non-moving reference frame is always different from that of NM. Let a NM velocity be denoted by V´=x´/t .
V´ = x´/t = (x´/I)c , (13)
so V´/c = x´/I . (14)
Let the SRT velocity be denoted by v . In SRT, there are two times, t and t´ , the t´ being attributed to the moving reference frame. So the SRT velocity in the primed system is:
v´ = x´/t´ = [x´ / (ct´)]c = (x´ / H´)c , (15)
v´/c = x´/ct´ = x´/H´ . (16)
2.5 The γ and Velocity in NM and SRT
Given
V = γv , or v = V/y , (17a,b)
and
γ = H´/I = (ct´)/I (SRT) = (c´t)/I (NM) (17c,d)
the equivalence of γ to H /I is completely accurate. (Proof in Appendix 1.) In NM, H´ has numerical value c´t . In SRT, H´ has numerical value ct´ . The numerical value of γ is the same in both NM and SRT because the value of (H´)2 is the same in both, (x´)2 +I2 . The numerical value of ct´ in SRT equals the numerical value of c´t in NM. So the SRT version of γ satisfies:
_________
γ´ = 1 / √ 1 – (v/c)2 = (ct´)/I = H´/I . (18)
The NM version of γ satisfies
γ´ = (c´t)/I = H´ /I . (19)
By Eqs. (17), (2), and (14), γ2 is
(γ´)2 = (H´)2 / I2 = [(x´)2 + I2]/I2 = (V´/c)2 + 1 . (20)
This shows that γ , usually thought of as applying only to SRT, is also a function of NM velocity. In NM, Eqs. (14) and (16) imply Eq. (18), and together they imply:
V´/c = x´/I = [(ct´)/I] (x´ / ct´) = (H´/I)(x´/H´) = γ(v´/c) = x´/I . (21)
The V´/c of NM equals the γ(v´/c) of SRT! They both equal the ratio of the distance the object moved in the un-primed, non-moving reference frame, x´ , to the distance the light moved in the unprimed non-moving reference frame, I .
The traditional way of reckoning velocity using a timing signal of known speed in its reference frame is the ratio of the distance moved by the object in that reference frame to the distance moved by the timing signal, times the speed of the timing signal, or, by Eq. (21),
(x´/I)c = V´ = γv´ . (22)
Note that the speed ratio x´/I can be far greater than 1.0, and γv´ can be far greater than 1.0, but if you check the math, v´ , the SRT 'velocity', can never be greater than c , because, by Eq. (16),
_________
v´/c = x´/ct´ = x´/H´ = x´ / √ (x´)2 + I2) , (23)
although x´/I approaches infinity as v´/ c approaches 1.0 because of the gamma factor, γ . So much for, "Nothing can go faster than c .” Just not true.
2.6 NM & SRT Transformations from Interval Equation
The NM transformation equation
x´ = V´t + x (24)
can be derived using only the NM Interval Equation (IE), Eq. (7). The variables used are x´ , I (which includes c and t ), and x . The transformation equation involves IE quantities and V , and from (24), V=c(x´–x)/I , also only IE quantities. Therefore, the NM transformation equation derives from its IE. (It’s 'inverse' transformation equation is just x = x´ –Vt .)
The SRT transformation equations,
x´ = γ(x + vt) = γ(u/c)ct + γx , (25)
and t´ = γ[t + (v/c2)x] ; ct´ = γet + γ(v/c)x , (26)
can be derived using only the SRT Interval Equation. This derivation is in Appendix 2.
The 'inverse' SRT transformation equations view the 'prime' reference frame as the non-moving frame; they are not simply moving x and x´ to opposite sides of the equation. The 'inverse' SRT transformation equations are
x = γ(x´ – vt´) = γx´ – γ(v/c)(ct´) , (27)
t = γ[t´ – (v/c2 )x´ ] , ct = γct´ – γ(v/c)x´ , (28)
and need no further discussion.
2.7 Going From NM to SRT
Because both NM and SRT derive from the same Interval Equation, (x´)2 +I2 = H2 , there is a 1:1 correspondence between the NM and the SRT depictions of any physical manifestation, and each depiction can be converted (accurately) to the other.
To convert the NM depiction, Eq. (24), to the SRT depiction, Eqs. (25 & 26):
1. Replace the SRT x with the NM x value.
2. Replace the SRT γ(v/c) with the NM value (V´/c) .
__________
3. Replace the SRT γ with the NM value √(V /c)2 + 1 .
4. If x = 0 , use the NM value ct in both SRT equations.
_________
5. If x ≠ 0 , replace the SRT ct with the NM value √(ct)2 + x2 .
_________
Using NM √(ct)2 + x2 instead of just ct is necessary because I2 must be the same in all reference frames and, if x ≠ 0 in the NM depiction, then the “c´t” of NM must be increased so both (ct)2 – x2 of NM, Eq (24), and (ct´)2 – (x´)2 of SRT, Eqs. (25) & (26), equal I2 . If the NM x = 0, then the SRT x´ equals the NM x´ ; otherwise, not.
2.8 And From SRT to NM
To convert the SRT depiction, Eqs. (25) & (26), to the NM depiction, Eq. (24):
1. Solve for all the variables of Eqs. (25) and (26).
________
2. Replace NM value V´/c with the SRT √(γ´ 2) – 1 .
__________ ________
I = √(ct´)2 – x´2 = √(ct)2 – x2
3. Replace NM ct with the value of I .
4. Replace NM x with SRT x , if it is known; otherwise:
5. If x´– γ´(v´/c)(ct) = 0 , then x=0 in Eq. (24), and the NM x´ equals the SRT x´ .
6. If x´– γ´((v´/c)(ct) ≠ 0, then in Eq. (24),
________
x = γx´ – (ct´)√(γ´)2 – 1 . (29)
from Eqs. (24) and (26), and the NM x´ does not equal the SRT x´ , but can be calculated from the NM variables already obtained.
3. Discussion
3.1 SRT Converts to NM, & vice versa
It has long been thought that SRT is the accurate portrayal of the world for inertial reference frames, and that, although NM was wrong, NM was sufficiently accurate for speeds much lower than the speed of light c . However, the fact that NM and SRT can both be derived directly from Eq. (2) proves that SRT is a 1:1 mathematical ´translation´ of NM. SRT can be considered an encryption of NM. This is further shown in Sections 2.7 & 2.8, which convert SRT into NM and vice versa. To become convinced, just put numbers into these equations. Every depiction of a moving object based on using light as a timing signal can be done in either SRT or NM, and either depiction can be converted accurately to the other.
Energy, momentum, collisions, etc., are merely other functions of space, x, y, z, and time, t , plus rest mass, a constant, so they are also convertible between NM and SRT, although they come up with different numbers, such as the V of NM equaling the γv of SRT. However, since every SRT depiction can be converted to a NM depiction (and vice versa), why ever use SRT, which commingles time and space, rather than NM, which doesn’t, and is much simpler. (Honestly, do you really understand ´dilated´ time, even when it reverses based only on which reference frame you choose to call moving?)
3.2 SRT Derives from NM as Follows:
After the time t , the portion of the light moving perpendicularly (as well as all other directions) to the object’s motion has moved the distance I , based on I=ct for x=0 . The x=0 implies the perpendicularity. Eq. (2), the Interval Equation for both SRT and NM, states that after time t the object now at x´ is now further from the light than the distance x´ . NM simply acknowledges that if (I/t)=c , then (H´/t)>c ; call it c´ , Eq. (5). However, Einstein´s Second Postulate says that the ratio of distance H´ to time t , the speed of the light relative to the object now at x´ , must also be c in the object’s (and every other) reference frame. Since H´≠ct , the only way to have an equality involving H´ and c is to change the time t as needed to accomplish this. Thus, although H´ has the same numerical value in SRT as in NM, the equation is changed to H´= ct´ , Eq. (9). This change from Eq. (5) to Eq. (9) is the entire basis of SRT. This change in the Interval Equation is what creates the SRT transformation equations and all the relativistic concepts, vs. the NM transformation equations and classical Galilean concepts. See Appendix 2.
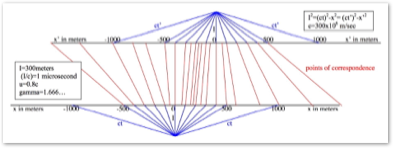
3.3 A Numerical Example
Suppose an omni-directional light is turned on just as an object (at x=0 in its reference frame) moves past at 0.8 c (SRT velocity). How far has the object moved after 1 microsecond (1 µsec)? After one µsec the light has moved the distance I= ct = 300 m. For (v/c)=0.8 , Eq. (17) gives:
_________ _________
γ = l/√ l – (v/c)2 = l/√ l – (16/25) = 5 / 3 .
The SRT transformation equation, Eq. (25), gives:
x´ = γ[x + (v´/c)(ct)] = (5/3)(0.8 x 300) = 400 m
So the light has traveled I = ct = 300 x 106 m/sec x 10–6 sec; i.e., I = 300m , and the object has traveled x´ = 400m .
x´/I = (400 / 300) = γ(v´/ c) = (5 / 3)(4 / 5) = 4 / 3 = V´/c ,
i.e., the NM velocity is 1.33... c , the ratio of the distance the object traveled to the distance the timing signal, light, traveled, times the speed c of the light timing signal. By Eqs. (21) & (20)
___________
v´/c = V´/cγ = V´ / c √ (V´/c)2 + 1 .
So why bother with SRT, when NM does the same job without intermingling time with space? The NM version of this same physical situation is
x´ = V´t + x = (V´/c) ct + x = (4/3) x 300 + 0 = 400m ,
just as with SRT. Of course, there is no ‘dilated’ time to consider. Without going into the unnecessary complications that would arise if considered in SRT, if there were another object that was, and stayed, 100m in front of the object just considered, the new x´ would be 400m +100m = 500m, and the x value would 100m. Why even bother with SRT? It is just a 1:1 mathematical transformation of NM, as exemplified by this numerical example, and by SRT’s own equations, examined in this paper.
3.4 No Time Dilation or Length Contraction
As discussed above, every SRT depiction can be converted to a NM depiction. ‘Time dilation’ is a fiction created by insisting (postulating) that Eq. (5) from Eq. (2) be changed to Eq. (9) to solve the problem that obviously (H´/t) > (I/t) because of x´ .
Since the same SRT physical situation can be depicted in NM without ‘time dilation’, the ‘time dilation’ and its corollary, ‘length contraction’ in SRT are simply mathematical artifacts, not physical realities.
3.5 There Can Exist Multiple SRT´s
SRT is based on the idea that something can have the same speed in both of two reference frames moving with respect to each other. Einstein´s Second Postulate and his transformation equations indicate this. However, the same equations result for whatever you postulate, insist, etc., that it moves the same speed, whatever speed you choose, in both of two reference frames moving with respect to each other. Whatever value is chosen for that speed (the equivalent of c for light), changing from Eq. (5) to Eq. (9) will result in all the SRT equations and concepts.
3.6 Why c is the Speed Limit in SRT
Eq. (23) shows why, according to SRT, nothing can go faster than light speed c . SRT ‘time’ is a function of NM time (SRT ‘proper’ time is the same) t=Ilc , modified Eq. (3), and also location and velocity, as shown in Eq. (26). The one SRT function that is a function only of time (NM time at that) is t=I/c , not the so-called ‘time’ set out in the SRT transformation equation, Eq. (26). SRT velocity is distance traveled divided by the ‘dilated’ time of SRT, resulting in Eq. (23) which shows why nothing will ever show an SRT velocity v/c greater than 1.0 .
3.7 Objects Can Travel Faster Than c
The transformation equations of both SRT and NM which give their definition of velocity, have been derived in this paper from only the Interval, Eq. (2). A reasonable definition of velocity using a timing signal of known velocity in a reference frame is the ratio of the distance traveled by the object to the distance traveled by the timing signal (e.g., light) times the velocity of the timing signal; i.e., Eq. (22):
(x´/I)c = γv = V .
The v is the SRT speed, and the V is the NM speed; they are not the same thing. Again, note that (x´ /I)c and γv can approach infinity in both SRT and NM, as can the NM V, although v will always be < c and (v/c) < 1.0 . Those who have tried to find ways to get objects to have (v/c) > 1.0 have, of course, failed, because they did not understand the purely mathematical nature of the SRT definition of velocity, Eq. (23). Eq. (21) shows that the statement that no object can have a speed greater than c is false by any meaningful concept of speed.
3.8 NM Keeps Space & Time Separate
Although problems involving objects moving in relation to each other over time using something of known speed in a reference frame as the source of the time, e.g., light, can be done equivalently in either NM or SRT, NM keeps the concepts of space and time separated, the way we normally experience them. SRT mixes the concepts together in a manner that seems mysterious. SRT time, except for ‘proper time’, is a function of velocity and distance as shown by Eq. 26. The γx of Eq. (25), rather than just x , is another example of this. Since any such problem can be done in NM by using Sect. 2.8, keeping space and time separate and understandable, it seems silly to use SRT.
3.9 The Twins Paradox
The Twins Paradox arises when the moving and non-moving reference frames are switched. Then t=I/c is measured in the formerly moving reference frame and the time is ‘dilated’ in what was the non-moving reference frame. Whether the time is ‘dilated’ or not depends on which reference frame you choose for the light timing signal. This again illustrates that the time ‘dilation’ of SRT is mathematical, and not real. The correct answer is that the twins are the same age, t=I/c , by correctly measuring only time in whatever reference frame the light traveled I=ct .
3.10 Mass-Energy Equivalence: E = mc2
Nothing in the Universe has velocity or kinetic energy in and of itself. Everything in the universe has velocity and kinetic energy relative to everything else in the universe except those objects not changing distance with it over time. So if mass is a function of (kinetic) energy, E=me2 , as Einstein believed, then everything would have an infinite number of 'masses'. The correct equation according to SRT is E=γm0c2 , where m0 is the so-called ‘rest mass’, and γ is the SRT gamma factor, which depends only on speed. Einstein thought mass actually changed with velocity. The correct E=γm0c2 can be obtained simply by multiplying the SRT Interval Equation, Eq. (11), by (me /I)2 :
(γme2)2 = (Pc)2 + (me2)2 , which is E2 – (Pc)2 = (E0)2 ,
where E = γmc2 , P is momentum, and E0 = me2 is SRT rest-mass energy.
4.0 Conclusion
SRT has been shown to be a simple mathematical translation, or encryption, of ordinary NM, Eqs. (2)-(12). The distance x´ that an object moves while the light moves I = ct is the NM velocity ratio V/c in NM, but in SRT is γ(v / c) , rather than the SRT velocity ratio v/c , Eq. (21). Time-distance-velocity problems can be done accurately for different reference frames by using either SRT or NM, but the SRT results commingle space, time, and velocity with each other in a confusing way. It has been shown how to accurately convert the SRT depiction to the NM depiction at any speed, and vice versa, Sections. 2.7 & 2.8.
Time dilation, its corollary length contraction, and the speed maximum c, are not physical realities, but rather mathematical creations, resulting from Einstein's Second Postulate that something (light) can travel the same speed in both of two arbitrary reference frames moving with respect to each other. To further illustrate the mathematical, rather than physical, nature of SRT, his postulate can be applied to anything at any speed, and the same SRT equations and concepts result no matter what the something is, or what its ‘same speed in both arbitrary reference frames moving with respect to each other’ is. The value of ‘c’ is merely changed to that speed and the equations will be the same, Eqs. (2)-(12). Einstein's idea that mass changes with kinetic energy was wrong, even according to his own SRT theory. The equation E=me2 should read E=γmc2 .
NM tells us nothing about light, except to use it as a timing signal if it travels at I = ct in its own reference frame. SRT says a lot about light, including that all observers (receivers) will find light arriving at speed c . However a distant receiver might change his speed after the light has left its source. How will the light then ‘know’ to adjust so that it still arrives at the receiver at speed c ?
Incidentally, round trip light speed has been measured on earth many times, always getting the same result. However, if light actually traveled near Earth at speed c relative to, say, the axis (magnetic field?) of Earth, rather than its surface, the difference between the round-trip measured speed, cm, and the real speed c would be:
cm = 2x/(t1 + t2) = 2x / [x /(c + V) + x/(c – V)] = 2(c2 -V2)/2c = c[1 – V2/c2] .
Since the speed of rotation of Earth's surface is about 460 m/sec , compared to the almos almost 300 x 106m/s measured speed for light, V2/c2 = 2.3511 x 10–12 . Because the measured speed, cm , is a ‘round-trip’ speed, the actual speed c is greater, but only by about 0.7 millimeter/sec.
Appendix 1: Various Meanings of the SRT γ
The SRT Interval Equation is:
I2 = (ct)2 – x2 = (ct´)2 – (x´)2 = (ct´´) – (x´´)2 = (ct´´´)2 – (x´´´)2 =... (Al-1)
The SRT transformation equation for x´ is:
x´ = γ(x + vt) = γx + γ(v/c)(ct) . (Al-2)
Considering Eq. (Al-2) and the origin x = 0 of the non-moving reference frame,
x´ / ct = x´ /I = γ(v/c) , (Al-3)
and, in NM, with x = 0 , x´=Vt=(V/c)(ct) , and by Eq. (1) in the main paper
x´/(ct) = x´/I = V/c , (Al-4)
so NM velocity V equals SRT velocity v times γ :
V = γv . (Al-5)
When x = 0 , the SRT γ is:
_________
γ = l / √ l – (v/c)2 , (Al-6)
so
γ2 = 1 / [1 – (v/c)2] . (Al-7)
Multiply numerator and denominator of Eq. (Al-7) by (ct´)2:
γ2 = (ct´)2 / [(ct´)2 – (ct´)2 (v/c)2] , (Al-8)
γ2 = (ct´)2 / [(ct´)2 – (ct´)2 (x´/t´c)2] , (Al-9)
γ2 = (ct´)2 / [(ct´)2 – (x´)2] , (Al-10)
γ2 = (ct´)2/I2 . (Al-11)
Therefore, the γ given by Eqs. (Al-11), (Al-5), & (Al-1), also satisfies:
γ2 = [(x´)2 + I2]/I2 = (V/c)2 +1 = γ2(v/c)2 +1 ; (Al-12)
γ´ = (ct´)/I ; γ” = (ct”)/I ;… (Al-13)
When x = 0, _________
γ = 1 / √ 1 – (v/c)2 . (Al-14)
All of the above assumes x=0 , meaning one is measuring from the zero point of the non-moving reference frame, the point where the light timing signal originates and the movement of the zero point of the moving reference frame begins. If one measures from another point in the non-moving reference frame, meaning that x≠0 , then from Eq. (Al-2)
γ = x´/ [(v/c)(ct) + x] . (Al-15)
However, if x≠0 , then ct≠I . The definition of γ , in terms of I instead of ct , is
_______
γ = x´ / {(v/c)I + [(v/c)(√x2 + I2 – I) + x]} , (Al-16)
where everything in the square brackets is due to x. If x = 0 , then (Al-12) and (Al-13) hold as before:
γ = V´/v´ = (x´/I)/(x´/ct´) = ct´/I . (Al-17)
Appendix 2: Deriving the SRT transformation equations from the SRT Interval equation
One central concept of SRT theory is the SRT Interval equation
I2 = (ct)2 – x2 = (ct´)2 – x´2 = (ct´´)2 – x´´2 = … (A2-1)
The unprimed frame is the non-moving frame. The four SRT coordinate transformation equations follow from this. One of these can illustrate the pattern:
x´ = γ(x + vt) = γx + (v/c)ct . (A2-2)
The purpose here is to derive this SRT transformation equation using only some or all of the variables in the SRT Interval Equation
I2 = (ct)2 – x2 = (ct´)2 – x´2 . (A2-3)
The I2 is easily calculated from any three of the other variables. So any three of the variables suffice to produce Eq. (2), the SRT transformation. For convenience, define a variable
z = V/c = γv/c (A2-4)
where V is velocity in Newtonian Mechanics (NM), c is the speed of light, v is SRT velocity (not the same as NM velocity V except at v=V=0) , and γ is the SRT gamma factor:
γ = 1/(1 – (v/c)2)1/2 = (( V/c)2 +1)1/2 = (z2 + 1)1/2 = ct´/I . (A2-5)
Eqs. (A2-4,5) were derived in Appendix 1.
Using Eqs. (A2-4) and (A2-5), Eq. (A2-2) can be written
x´ = zct + x(z2 +1)1/2 . (A2-6)
The variables other than z are given from the SRT Interval equation Eq. (A2-1), so when z is found in terms of only quantities found in Eq 1, the derivation of the SRT transformation equation from the SRT Interval Equation is complete. From Eq. (A2-6)
(z2 +1)1/2 = (x´ – zct)/ x (A2-7)
z2 +1 = [x´2 – 2x´ctz +(ct)2z2]/x2 (A2-8)
z2 = [x´2 – 2x´ctz +(ct)2z2 – x2]/x2 (A2-9)
x2z2 = x´2 – 2x´ct z +(ct)2z2 – x2 (A2-10)
(x2 – (ct)2)z2 + 2x´ct z – x´2 + x2 = 0 (A2-11)
((ct)2 – x2)z2 – 2x´ct z + (x´2 – x2) = 0 (A2-12)
From (A2.1), (ct)2 – x2 = I2 , and
I2 z2 – 2x´ct z + (x´2 – x2) = 0 (A2-13)
which is a quadratic equation for z , so we can consider
z = (V/c) = γ(v/c) = [2(x´)(ct) ± (4(x´)2(ct)2 – 4I2(x´2 – x2))1/2] / 2I2 (A2-14)
z = ( V/c) = γ( v/c) = [x´(ct) – (x´2(ct)2 – I2(x´2 – x2))1/2] / I2 (A2-15)
z = ( V/c) = γ(v/c) = [x´(ct) – (x´2((ct)2 – I2) + I2x2)1/2] / I2 (A2-16)
z = ( V/c) = γ(v/c) = [x´(ct) – (x´2x2 + I2x2)1/2] / I2 (A2-17)
z = ( V/c) = γ(v/c) = [x´(ct) – x(x´2 + I2)1/2] / I2 (A2-18)
z = ( V/c) = γ(v/c) = [x´(ct) – x(ct´)] / I2 (A2-19)
γ2 = ( V/c)2 + 1 = ( γv/c)2 + 1 = [(x´(ct) – x(ct´))2 / I4] + 1 (A2-20)
All quantities on the right are obtainable from the SRT Interval equation. By Eq. (A2-6)
x´ = zct + (z2+1)1/2 x (A2-21)
And, using the relationships
x´ = γ(x + vt) , (ct´)2 = I2 + x´2 (A2-22, 23)
The SRT transformation equation for ct´ is
ct´ = (z2+1)1/2 ct + zx (A2-24)
or ct´ = γct + γ(v/c)x ; t´= γ(t + (v/c2)x , (A2-25)
the latter being the usual form. The quantity ct´ can also be found from Eq. (A2-23).
From Eqs. (A2-22) and (A2-25) the other two (reverse) SRT transformation equations can also be derived, showing definitively that the four SRT transformation equations derive directly from the SRT Interval Equation.
Additionally, the SRT Interval equation can be derived from the SRT transformation equations. If we subtract (x´)2 from (ct´)2 , nearly everything cancels, and we have only the SRT Interval equation, i.e.,
ct´2 – x´2 = ct2 – x2 = I2 (A2-26)
Appendix 3: A Pictorial Approach [not needed]
The End of Special Relativity Theory
Published in Galilean Electrodynamics July/August 2020; Vol. 31 No.4
Dr. Sherwood Kaip
email <skaip799@gmail.com; cell (915) 309-6340
To return from PRINT page, click "back" arrow on your browser