On the Multiple Meanings of 'Time' in SRT
Dr. Sherwood Kaip
El Paso, TX
This material may be reproduced if author attribution is given.
C A U T I O N:
Do not attempt to print this screen. Use the 'print version'. From this screen the gamma function (c) prints as 'c' and italics, superscripts and subscripts are printed improperly as well. The article will be unitelligible. Use the 'print version' to print.
This article will use only the equations of Special Relativity (SR) to examine the exact and unusual nature of time in Special Relativity (SR). Comparisons will be made with certain aspects of Newtonian Mechanics (NM).
2. Conceptula Analysis
Let two events occur a time apart in two locations in a reference frame. As examined and described in Newtonian Mechanics (NM), these events will occur in different locations in other reference frames moving with respect to the first. However, according to Newtonian Mechanics (NM), the time of the events will be the same in all reference frames including those moving with respect to the first.
As examined and described in Special Relativity (SRT), these events will occur in both different locations and different times in other reference frames moving with respect to the first. This is called time dilation. However, there is another Special Relativity (SRT) quantity which, just like the time of Newtonian Mechanics (NM), has the same value in all reference frames. This is called the relativistic Interval (I), defined by Eq. 1 below. Furthermore, by Eq. 1a, (I/c) is the same, both qualitatively and quantitatively, as the time of Newtonian Mechanics (NM). This will be demonstrated and its consequences evaluated in what follows. The equations of Special Relativity (SRT) follow:
Eq.1
Eq. 1a
Eq. 2
Eq.3
Eq. 3a
Eq. 3b
Eq. 4
Eq. 4a
Eq. 4b
Eq. 5
Eq. 5a
Eq. 6
Eq. 6a
Eq. 7
Eq. 7a
Eq. 8
Eq. 8b
Eq. 9
Eq. 9a
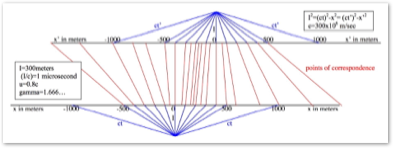
Reference frames moving past each other linearly (inertial) in any direction may always be converted to a movement in the x direction by rotating the coordinate axes. Therefore, all subsequent discussion will consider all motion between reference frames to be in the x direction. In these discussions, it will be assumed that the first event occurred at x=x´=t=t´=0. At this point a light signal starts out at speed c from x=x´=0. The second event will occur later as measured by the distance the light has traveled in the reference frame in which it was emitted. When light is emitted in a reference frame from a source which is not moving in that reference frame, the portion of the beam perpendicular to the direction of motion of other reference frames does not change its x position in its reference frame over time, i.e., x=0 and remains so in that reference frame.
By Eqs. 1 and 1a, if the x value in a reference frame is 0, then the relativistic Interval (I) is the distance ct that the perpendicular ray of the light emitted in that reference frame travelled perpendicularly. In this case I/c is the time it took the light to travel that distance at speed c. This time in SRT is called ‘proper time’. This is also the same exact way that time would be expressed in NM.
3. Mathematical Description
Call this reference frame the unprimed frame. Then all other reference frames moving in the x direction will have an x value at time t. By Eq. 1, if the primed reference frame moved x´ distance during time t, then
(ct´)2 = I2 + (x´)2
If the double-prime reference frame moved x´´ distance during time t, then
(ct´´)2 = I2 + (x´´)2
And so on for all other possible reference frames moving an infinite possible number of different distances during the time t or I/c. Again, I/c is the time the light took to travel the perpendicular distance (I) in the reference frame in which it was emitted from a source not moving in that reference frame. It traveled that same perpendicular distance in all possible other reference frames moving in the x direction at different speeds as shown by Eqs. 1.
A look at Eq. 1 shows that (ct´), (ct´´), (ct´´´) or whatever is a combination of a reference frame’s movement in the x direction with the perpendicular distance (I) that the light has traveled in all reference frames (at speed c). I.e., (ct´), (ct´´), (ct´´´), etc. is the vertical plus horizontal distance the perpendicular light ray in the ‘proper time’ frame has traveled in these other reference frames. Obviously these distances are greater than (I).
These distances are the same as would be calculated in NM, but in NM one would simply say that the speed of the light is greater in these other reference frames than the speed c of the perpendicular light ray in the reference frame in which the source is not moving because the distance traveled by the perpendicular light ray in these other reference frames is greater due to the horizontal x movement in addition to the vertical distance (I).
However, SRT stipulates that c is the same in all reference frames. So in order to keep the c, the ratio of the distance the light ray moved in a reference frame to the time of that movement in the same reference frame, constant, the t in these other reference frames must be increased. This is the basis of ‘time dilation’ in SRT.
The basis and validity of Eq. 1 is easily shown by multiplying Eq. (4) by c, squaring the result, and subtracting the square of Eq. 3. The algebraic cancellations are a little complicated but Eq. 1 is what will result. (The transform Eqs. 3-6 can also be derived from Eq. 1.)
Henceforth, I will refer to the ‘proper time’ reference frame as the non-moving reference frame. This means that in Eqs. 3 & 4 (and 5 & 6), the x on the right side of the equals sign is equal to zero. Eqs. 2 & 4a thus show that when x=0,
𝛾 = ct´/ct = ct´/I
(Eqs. 2 & 6a shows that, correspondingly, when x´=0,
𝛾 = ct/ct´ = ct/I
The distances ct´ and I are the same in NM, so 𝛾 is exactly the same, both qualitatively and quantitatively, in SRT and NM. The difference between SRT and NM is that NM would call the distance c´t or c´(I/c) where c´ is the greater distance divided by the same time as found from (I), whereas SRT calls the same distance ct´.
u is the relativistic velocity between reference frames. Eq. 7a shows that u´/c equals the distance traveled by the reference frame divided by the distance the ‘proper time’ perpendicular light ray traveled in that frame, i.e.,
u´/c = x´/ct´ or u´´/c = x´´/ct´´,
or whatever for other moving reference frames. This may seem an unusual way to define velocity between reference frames but that’s the way it works in SRT.
In NM, velocity between reference frames would be defined as, e.g.,
v´´´ = x´´´/t = x´´´/(I/c) and v´´´/c = x´´´/ct = x´´´/I.
In other words, v/c is the ratio of the distance the various reference frames traveled in the x direction to the distance the perpendicular light traveled in all reference frames.
Looking at Eq 3a where the non-moving reference frame is on the right of the equals sign, the distance x´ that the prime frame traveled past the non-moving reference frame point x=0 is not the SRT velocity u times the time t but is 𝛾 times the SRT velocity u times the time t (or, alternatively, I/c). This can also be expressed as
x´ = 𝛾(u/c)ct or x´ = 𝛾(u/c)I.
The situation with x´=0 and Eq. 5a is similar.
The NM version of this is: “the distance x´ that the prime frame traveled past the non-moving reference frame is the NM velocity v times the time t (or I/c). This can be expressed as
x´ = vt or, alternatively,
x´ = (v/c)ct = (v/c)I.”
So in NM (v/c)=x´/I. Thus, the ratio of the distance the moving reference frame traveled to the distance the light traveled in the non-moving reference frame is 𝛾(u/c) in SRT and (v/c) in NM. However, as described above, 𝛾=ct´/I and (u´/c)=x´/ct´ and therefore
𝛾(u/c) = (ct´/I)(x´/ct´) = (x´/I) = (v/c).
Thus (v/c)=𝛾(u/c) and the NM velocity v is the same as the SRT velocity u times 𝛾. In other words, the NM velocity is the distance the moving frame moved divided by the time (‘proper time’ of SRT) the light moved the distance (I) perpendicularly at speed c; and the SRT velocity u times 𝛾 is that same number.
Especially notice that the distance the moving reference frame traveled can easily be far greater than the distance (I) the perpendicular light was able to travel at speed c (in all reference frames) and this is true for both the SRT and the NM viewpoint. Yet the SRT ‘velocity’ u will always be less than c because of the mathematical nature of (𝛾u). This is seen readily by noting the definition of SRT velocities u/c in Eqs. 7 and recognizing that, by Eq. 1, since, e.g., I 2 + x´´´2 = (ct´´´) 2, any (u/c) is equivalent to dividing the side of a right triangle (the x distance x´´´) by its hypotenuse, ct´´´, which will always be less than 1.0.
All the above has demonstrated that, by examining only the equations of SRT, the following can be deduced:
A light pulse traveling a distance I=ct in a (‘non-moving’) reference frame will travel a greater distance in a reference frame moving perpendicularly to it, namely, the vector sum of the distance (I) the light pulse traveled at speed c during the time t in this and all other reference frames, and the perpendicular distance the particular reference frame moved relative to it during that same period I/c=t.
NM agrees exactly with the previous paragraph. NM considers the increased distance covered in the moving reference frame during the time I/c an increase in velocity for the light pulse (or anything else moving in that manner) relative to the other reference frame. SRT insists on holding constant the ratio (speed) of the increased distance covered by the light in the moving reference frame to the time (I/c) it took the light pulse to cover the distance (I) in the frame in which it was emitted. Since (distance / time) = velocity, the only way to keep the ratio of the known increased distance to time constant is to assign a larger number to the time. This is the basis of ‘time dilation’ in SRT and is why SRT and NM have different values for describing speed between reference frames. I have used u for the SRT value and v for the NM value of velocity.
For x=0, notice that by SRT in Eq. 3a
x´ = 𝛾(u/c)(ct) = 𝛾(u/c)I
and by NM in Eq. 9a
x´ = vt = (v/c)(ct) = (v/c)I = 𝛾(u/c)I
Both are accurately describing the same phenomenon by their respective ‘rules’. One can express the distance and speed one reference frame passed another during the time a light pulse traveled the distance (I) perpendicularly in both (and all other) reference frames either by SRT or NM. If one system is accurate, so is the other. (If one is wrong, both are.) Again notice that the distance x´ that the moving reference frame traveled past the non-moving reference frame can be far greater than the distance (I) that the light traveled in the non-moving reference frame and is the same according to either system. This ratio of reference frame travel distance to light travel distance is 𝛾(u/c), not (u/c). The SRT ‘velocity’ u will still be less than c and (u/c) will be less than 1.0. Of course the NM system is much easier to follow.
What if the x term on the right side of Eqs. 3 & 4 (and Eqs. 5 & 6) is not zero? It is not as simple as just changing x to a non-zero value to show where a point in the non-moving reference frame is in another reference frame. The relativistic Interval (I) must be the same as for when x is zero. So if x is increased from 0, ct must be increased as well to keep (I) constant; but now ct is no longer equal to (I). (Although ((ct)2 – x2) still equals I2. Eqs. 3b & 4b illustrate this.) The square root quantity is the new ct.
In NM, the X on the right in Eq. 9 is the equivalent of saying that if the rear of a train passed the station one minute ago and is now a mile away, the train is traveling 60 miles per hour and, if the train is 1/2 mile long, the engine is at X=1/2 mile in the train reference frame and 1.5 miles in the station X´ reference frame.
In SRT, things are quite different. According to Eqs. 3 & 3b, an increase in x will cause a far greater increase in x´ than the increase in x. There will also be an increase in ct´ to keep (I) constant. Notice that the increase in x´ will always be greater than the increase in ct´ resulting in an increase in u´/c=x´/ct´. However, this increase will never cause u´/c to equal 1.0.
It turns out that the left side of both the x´ of Eq. 3 and the ct´ of Eq. 4 can be shown to be the sum of the motion of two reference frames both moving with respect to a non-moving reference frame, i.e.,
x´ = x1 + x2 and ct´ = ct1 + ct2
To do this, one must use (I) as shown in Eqs. 3b & 4b. The process works as follows. First, determine (I) from Eq. 1.
I = ((ct)2 – x2)1/2
Then
x1 = 𝛾(u/c)I and x2 = 𝛾(u/c)(ct – I) + 𝛾x and
ct1 = 𝛾I and ct2 = 𝛾(ct – I) + 𝛾(u/c)x
x1 and ct1 are Eqs. 3 & 4 for x=0 removed from the full Eqs. 3 & 4. x2 and ct2 are the remainder of Eqs. 3 & 4. (And “Eqs. 5b & 6b” could have been shown by switching primes and would be comparable.)
x1 and ct1 show the location, speed, etc. of the point x=0 in the prime frame. The 𝛾 in front of the x in Eq. 3 and the 𝛾(u/c) in front of the x in Eq. 4 are necessary to keep (I) the same on both sides of the equal sign in all the equations.
u’ is the sum of u1 and u2 calculated according to Eqs. 8.
This problem of the distance, time, and speed changes when both variables x are not zero disappears when the NM transform equation is derived (only) from the equations of SRT. In the resulting NM equation, (Eqs. 9), physical distances do not vary between reference frames. This can be found in an article on the Internet at <trybasics.com> in the Special Relativity section referred to as ‘NM from SR’ and titled “How to Derive Newtonian Mechanics Directly from Only the Equations of Special Relativity”. Accessed 7/30/17. A distance change in one reference frame simply causes an equal change in another.
Notice that these equations of SRT have described light as moving the same speed in all reference frames, which reference frames are moving with respect to each other at varying speeds. SRT does this by changing the use of ‘time’ which is different in each reference frame. However there is nothing in these equations that applies to light per se. Anything that was assumed, postulated, stipulated, or whatever, to travel the same speed in all reference frames would have to change the meaning of ‘time’ as described here and all the SRT equations and concepts would result! In addition, for the same reason, c need not be the speed of light. c could be any speed!
The only requirement for needing the equations of SRT to describe two events separated by space and time is to specify that something, anything, travels the same speed (any speed will do) in two reference frames moving with respect to each other. If this is done, all the equations and concepts of SRT follow directly. This fact shows that SRT is a mathematical construct, not a physical one. After all, almost by definition, anything moving at a particular speed in one reference frame will be moving at a different speed in a reference frame moving with respect to the first. This applies to light as much as anything else. A simple example will suffice.
If a train is moving forward at 4 ft/sec relative to the ground and raises a flag on the train straight up at 3 ft/sec, the flag is not moving with respect to the ground at 3 ft/sec. It is moving both vertically at 3 ft/sec and horizontally at 4 ft/sec resulting in an upward forward movement with respect to the ground of 5 ft/sec. If you insist that the flag is moving at 3 ft/sec in all reference frames, including relative to the ground, you will derive all the equations and concepts of SRT with the speed c = 3 ft/sec. SRT will agree with NM that the flag travelled 5 feet diagonally in the ground reference frame but, because it has been insisted (postulated, assumed) that the flag travels at 3 ft/sec in ground reference frame (and all others) as well as the train reference frame, it will say that the 5 feet traveled relative to the ground occurred over a time in the ground reference frame of 5/3 seconds. Since c must be 3 ft/sec,
u/c = x´/ct´ = 4/5,
u = (u/c)c = (4/5)c = 2.4 ft/sec.
And the other equations and concepts of SRT will emerge as follows:
Given: x=0, c=3 ft/sec, I=3 ft, x´=4 ft;
then by Eqs. 1 & 3:
t=1 sec, ct´=5 ft, t´=(5/3) sec,
u´/c = (x´/ct´) = 4/5, u´ = 2.4 ft/sec, 𝛾 = (ct´/I) = 5/3,
x´ = 𝛾ut = 𝛾(u/c)ct = 𝛾(u/c)I = (5/3)(4/5)3 = 4 ft.
It seems much simpler and of course just as accurate to use NM concepts. The flag is moving vertically in the train reference frame at a known 3 ft/sec and has moved 3 ft in that reference frame. Thus 1 second has passed. Meanwhile, the train moved 4 ft. Thus the train is moving at
v=x´/t=(4/1)=(v/c)c=(4/3)3=𝛾(u/c)c=(5/3)(4/5)3=4 ft/sec
and the flag is moving diagonally at 5 ft/sec relative to the ground. If you want to know where a point on the train 10 ft ahead of the flagpole is now, it is 10 ft ahead of where the flagpole is in the ground reference frame.
4. Conclusion
Both NM and SRT describe the space and time relationships between reference frames moving with respect to each other over time. They are 1:1 mathematical transforms of each other. Using SRT terms, NM time = I/c and NM velocity between reference frames is 𝛾u(I/c). As shown by the train example above, each SRT description of two events has exactly one NM description of those two events and vice versa.
It has not been recognized that the relativistic Interval (I), the distance light has traveled at speed c for time t perpendicular to all reference frames moving only in the x direction, has the same exact meaning, both qualitatively and quantitatively, in NM and SRT. And 𝛾, the ratio of the distance the light traveled in a moving reference frame to the distance (I) (see Eq. 2), also has the same exact meaning, both qualitatively and quantitatively, in NM and SRT. In addition, the NM velocity listed as v or (v/c) is the same as the SRT 𝛾u or 𝛾(u/c), resepctively. SRT velocity u/c between reference frames is always <1.0. However, 𝛾(u/c) is the ratio between the distance one reference frame traveled past another and the distance (I) that light traveled perpendicularly from its source during time t (at speed c) in both reference frames, and approaches infinity as u/c approaches 1.0.
Either the SRT or NM description can be used but NM is obviously simpler. Using the NM description makes it much easier to visualize exactly what is happening.
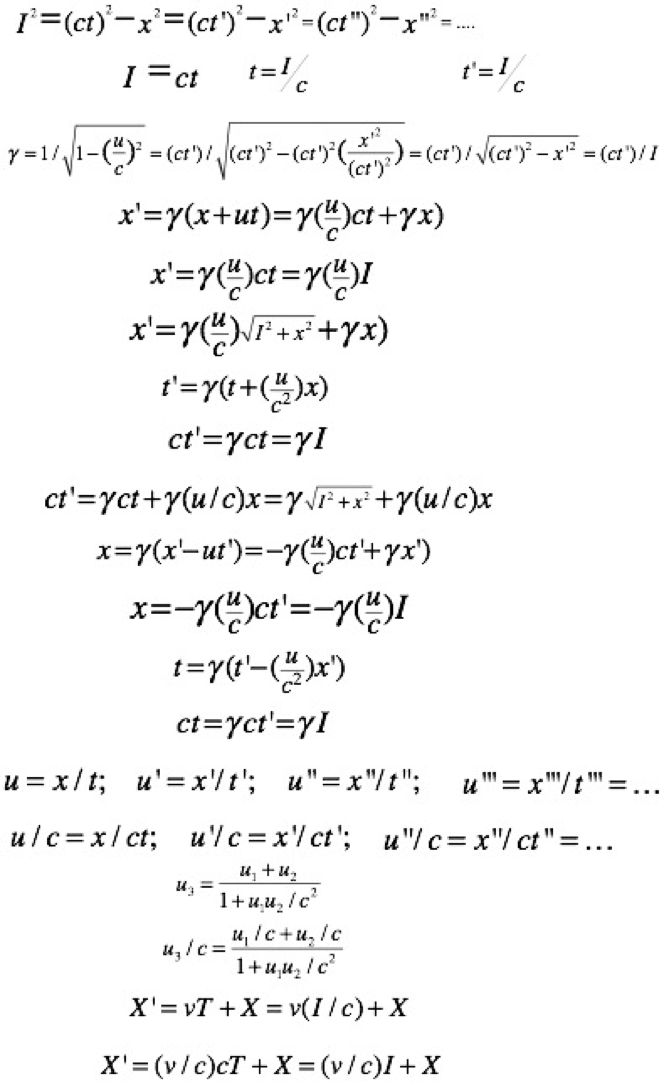
For x´=0
For x=0
For x=0
For x=0
For x´=0
For x´=0
For NM: