Correspondence Diagrams for NM and SR
by Dr. Sherwood Kaip; ©2006
Equations:
NM: X = vT + X’
SR: I2 = (ct)2 – x2 = (ct’)2 – x’ 2 𝛾 (gamma)=(1–(u/c)2) (–1/2)
x=𝛾(ut’ + x’)=𝛾(u/c)ct’ + 𝛾x’ ct=𝛾ct’ + 𝛾(u/c)x’
x’= 𝛾(–ut+x)= –𝛾(u/c)ct+𝛾x ct’=𝛾ct – 𝛾(u/c)x
Corresponding Points
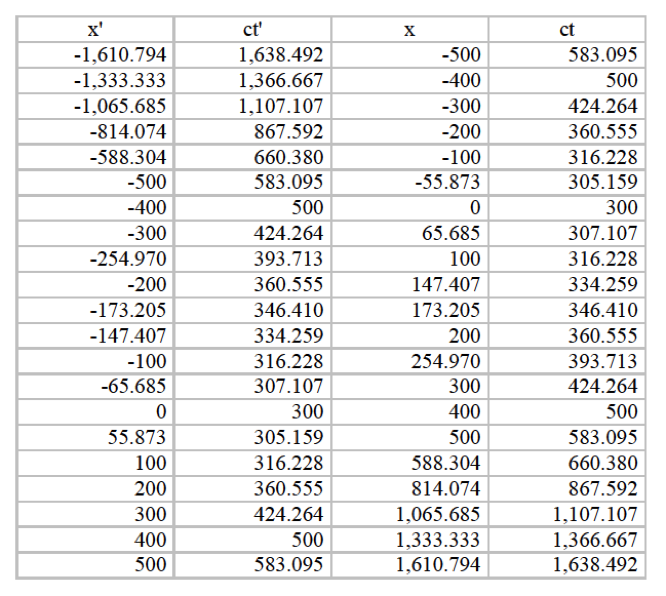
In Newtonian Mechanics (NM), the transform equations between reference frames is X=vT+X’ and the correspondence between reference frames can be shown as in the top diagram. Anything traveling out at speed c starting at T=X=X’=0 would be somewhere on the circle and meanwhile, in this case where v=(4/3)c and T=1 microsecond, the various values of x’ touching values of X would be as shown and as described by the transform equation. Therefore, X’=0 is at X=400 and other values of X’ are as shown in the diagram and the formula.
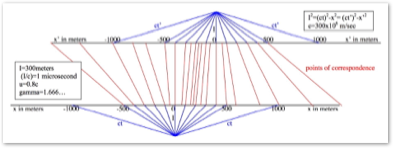
An equivalent Special Relativity (SR) correspondence diagram is shown second, above. Since in SR time is not constant between reference frames but the SR Interval (I) [defined in the upper right corner of the SR diagram] is, we will use I=300 meters as the Interval, which when divided by the constant c (speed of light) equals 1 microsecond.
The point x’=0 has traveled to x=400 meters in the unprimed frame. It has traveled 400m while something traveling at speed c has traveled 300 meters vertically. Although this might at first look like a speed (400/300)c or 1.333...c, in SR this works out to 0.8c because the time t at x=400 is 500/c as shown in the diagram and by the formula for ct, making u=x/t=0.8c.
The first event was when x’=0 was at x=0 and therefore t’ and t equalled zero also. This first event could be thought of as an explosion occurring at x’=0 and making a mark at x=0 and ‘starting the clock’ at that point. The prime reference frame is moving past the unprime reference frame at the SR velocity of u=0.8c. (As described in rel SR from NM and rel NM from SR and apparent in the NM diagram above, the NM velocity would be v=1.333...c.) The second event occurs when x’=0 is at x=400 meters. This second event could also be thought of as an explosion at x’=0 which leaves a mark at x=400 meters.
The Blue Lines and the Interval
Remember that it is a principle of SR that the SR Interval (I) between two events is the same in all reference frames moving with respect to each other. The black (distance) and blue (SR time) lines in the diagram show this. The blue lines for a given distance are a function only of the SR Interval (I) and have nothing to do with the relative speed between the reference frames. Thus at this second event where x’=0 is at x=400 m (and x=0 is at x= –400m), at all other values of x’ the time is different from 1 microsecond, and this is also true for x=0 where the time is also 1 microsecond but different at all other points of the unprimed frame.
This correspondence diagram would look exactly the same for t’=1 second (I=300 million meters) if the distance numbers are also multiplied by one million, e.g., x’=0 is at x=400 million meters. That is, both the vertical and horizontal scales are multiplied by one million. This would also be true for the red correspondence lines which show where the points of the prime and unprime frame ‘touch’ for the SR speed u=0.8c (which can be seen as ‘equivalent’ to the NM speed v=1.333...c). The angles of the red lines become more extreme for higher relative speeds. This diagram is constructed by using the Interval equation and the transform equations for I=300 meters and u=0.8c. The exact values are shown in the accompanying table.
For interest, the negative value of x’ which exactly corresponds to an equal but positive value of x is x= –x’=I((𝛾-1)/2)(1/2). As shown in the table, this is –x’=x=173.205.
The Correspondence of NM and SR
Keep in mind that the NM and SR correspondence diagrams above are describing the same physical phenomenon: two explosions at x’=0 one microsecond apart. In the SR case, the time of both the beginning and end of the interval is measured at the same point in the reference frame, namely x’=0. The time everywhere else in the prime reference frame is totally different, as shown and according to the SR Interval (I). Based on c=300 million meters/second, this time of t’=1 microsecond at x’=0 corresponds to an SR Interval of I=300 meters (and therefore (I/c)=1 microsecond), which I is the same at all points of the prime frame as well as the unprime frame and all other potential frames possible at various speeds. The ‘physical’ result of the two events is that x’=0 (and correspondingly x=0) travels 400 meters in both SR and NM. The time interval during which this happens is 1 microsecond in both SR and NM although that ‘time’ is the minimum amount of SR time shown only at x’=0 and x=0, yet it is the time resulting from dividing the SR Interval (I) by c, a time which applies to all possible variously moving reference frames just as the same NM time does. This difference in ‘time’ in SR and NM is mathematical, not physical.
What happened to x’=0?
Another interesting point. At the first event X’=X=T=0 in the NM diagram, it makes sense to speak of where non-zero values of X’ are, namely at the same value of X. In SR at the first event x=x’=t=t’=0, one cannot speak of where in the uprime frame non-zero points of the prime frame are located. At t’=0, any non-zero value for x’ results in a different value for the SR Interval, which means you are no longer referring to the same event. Furthermore, the SR Interval (I) for any such new event would be “space-like”, that is I2 would be negative.
However, if you accept t’ not being zero at values of x’≠0 when t’=x’=0, then ct’=x’ keeps the SR Interval (I) constant at 0. Then non-zero values of x’ would have non-zero values of t’ even though the time interval is just beginning at t’=0 at x’=0.
Summary
The above two diagrams show how the same physical situation is viewed in NM and SR. The first event, an explosion at X’=x’=0 that makes a mark at X=x=0 starts the clock at T=t’=0. The second event is an explosion at X’=x’=0 that makes a mark 400 meters to the right in the unprime frame (X=400 in NM and x=400 in SR) during an elapsed time of 1 microsecond as shown by the value of T or t’ at x’=0 or I/c. This time for the second event in SR is the only sensible one to use since the ‘time’ according to SR is different for each different location in the prime frame. Likewise for the unprime frame, the SR time t is 1 microsecond only for I/c and at x=0, being greater and different at each non-zero location in the unprime frame.
The point of all this is that any consideration of moving objects which can be done using SR can also be done using NM as recognizable in the above diagrams. Although time and distance can sometimes be the same in both NM and SR, note that the relative velocity between reference frames (objects) is never the same. The NM velocity, called v here, is the distance traveled by one point of one frame through the other divided by the time T, a quantity which is the same in all reference frames. In SR, that same NM velocity value equals the distance traveled by one point (x’=0 or x=0) of a reference frame through another reference frame divided by (I/c), a quantity which is also the same in all reference frames. However, this is not the velocity between reference frames as calculated for SR.
The SR velocity, called above by “u”, is u=x/t for x’=0 or –x’/t for x=0. In both cases, note that the time is larger than I/c. The full equations, equivalent to the NM version (v/c)=(X–X’)/(cT), is
(u/c) = (x – (x’/𝛾))/(ct) = – (x’ – (x/𝛾))/(ct’)
(Note that multiplying these equations through by 𝛾 yields the SR transform equations.) The velocity ‘v’ of NM is related to the SR velocity called ‘u’ in these papers by v=𝛾u as can be seen above.
SR can be derived directly from NM by assuming that something traveling at a known speed in a reference frame also travels at that same speed in another reference frame moving arbitrarily with respect to the first. This derivation is done in rel SR from NM. In rel NM from SR, the back conversion process from SR to NM is shown by deriving NM only from the equations of SR. Those two papers and this one show that any physical situation, even at high speed, can be viewed either via Newtonian Mechanics or via Special Relativity when the mathematical changes in meaning for time, distance, and velocity that occur in transferring from NM to SR are recognized.
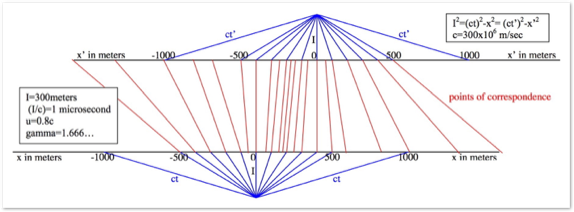
Movement as seen in Newtonian Mechanics (NM): Light travels 300m while object x’=0 travels 400m
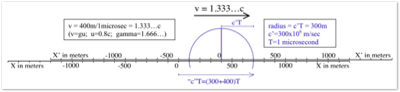
Same Movement as seen in Special Relativity (SR): Light travels 300m while object x’=0 travels 400m