A simple physical model involving only two moving objects and a timing signal of known velocity is examined both from a Newtonian Mechanics (NM) viewpoint and a Special Relativity Theory (SRT) viewpoint. This allows easy derivation of the equations of motion and seemingly unusual concepts of SRT. Concepts such as the twin paradox, why nothing can travel faster than light, the reason for time dilation, and others become clear and easily understood using this model. The similarities and differences between NM and SRT are examined and elucidated. For example, two important quantities thought to b exclusive to SRT are found to be exactly the same, both qualitatively and quantitatively, in NM.
1. Introduction
Many people have tried to show that Special Relativity Theory (SRT) is wrong. However, since it is internally consistent, it isn’t ‘wrong’. But it does come up with unusual concepts such as time dilation and its corollary length contraction. By carefully examining a simple physical situation, the exact nature of SRT can be clearly and easily understood as well as used.
Variables referring to Newtonian Mechanics (NM) will be in capital letters. Variables referring to Special Relativity Theory (SRT) will be in small case.
The symbol l is the point a timing signal of known speed has reached traveling along the vertical path I during the time T (or t). The letter c (or C) is used to represent the speed of the timing signal relative to other objects or reference frames and can be any speed, including the speed of light. The letters H, L, I will refer to distances which together form the sides of a right triangle and therefore H2 – L2 = I2.
Let us start by examining the physical situation from a Newtonian Mechanics (NM) point of view.
2. The Physical Situation in NM
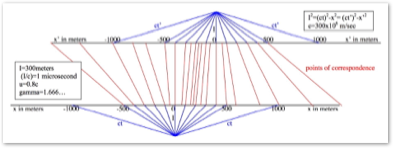
Fig. 1. Positions of x=0, x’=0, and 'timing signal' l after time T. In this Fig., ‘C’ has nothing whatever to do with light.
Fig. 1 illustrates the physical situation. Two reference frames are moving past each other in the x direction. The Cartesian coordinates can always be arranged so that the motion between inertial objects or reference frames is in the x direction.
Label one the unprimed frame and the other the prime frame. Although either frame could be the 'non-moving' frame, let us arbitrarily assign 'non-moving’ to the unprimed frame.
At time T = 0 and x = x’ = 0, a ‘timing signal’ l begins moving in the unprimed reference frame perpendicular to the relative motion between reference frames at a known, constant speed which in the diagram is called ‘C’. This speed, here arbitrarily labeled ‘C’, has nothing to do with light in this diagram. It does not matter what the signal is—it could be a constant speed rocket, or anything else. It does not matter what the constant speed is—only that it be in the perpendicular direction and that it be known. See Fig. 1.
The start of signal motion from x=0 at speed C is the first event. As the signal begins its travel from x = 0, it leaves a mark at the zero point of the unprime frame and also leaves a mark at x’ = 0 of the prime reference frame as it is passing by. Then at a later time, T (during which the ‘timing signal’ l has moved perpendicularly at known speed C a distance of CT), a mark is made again at the x = 0 point of the unprime frame and this mark also transfers onto the prime frame. This is the second event. But since the origin x = 0 of the unprime reference frame has moved right with respect to the primed frame the distance x’, the mark in the prime frame is at a distance labeled x’ to the right of x’ = 0, the latter now being at the lower left corner of the triangle as shown on Fig. 1. The NM transform definition is:
(5)
Since x for the second event is still at x = 0 for the unprimed reference frame, the velocity between these reference frames is in the x direction at speed v. The speed between reference frames normalized by the known signal speed C is:
(6)
or in terms of the triangle shown,
Irel (7)
Obviously, in the prime reference frame the ‘timing’ signal l has moved the vector sum of the vertical distance CT plus the horizontal distance x´ during the time T as shown in Fig. 1. This longer distance divided by the time T is the speed of the timing signal with respect to the prime reference frame and is denoted by C’ as shown in Fig. 1.
The distances traveled in three-dimensional space at known signal speeds C or C’ for time T are:
(8)
Rearranging,
, (9)
. (10)
Since there is no relative motion of the reference frames perpendicular to the horizontal direction x,
, (11)
and therefore
. (12)
Because x for the signal in the unprimed reference frame is still ‘horizontally’ at x = 0 at time T, x2 = 0 in Eqs.(9) and (12) so
, (13)
or, in terms of the triangle,
Irel 2 (14)
3. Definitions Common to SRT & NM
To really understand SRT it is crucial to know how two specific quantities thought to be only relativistic quantities actually have the same meaning in NM, both qualitatively and quantatively.
3.1 The relativistic Interval
First define a quantity called ‘Relativistic Interval’ Irel from
Irel 2 . (15)
Here Irel is obviously the perpendicular distance the signal traveled in both reference frames, i.e., the distance perpendicular to the relative motion of the reference frames.
Furthermore, if there had been another reference frame which had traveled a greater distance x´´ during the time T, then
Irel 2 (16)
and so on for any number of possible reference frames moving various distances during this time T. In other words, Irel is the distance perpendicular to the relative motion of the reference frames that the timing signal traveled in all possible reference frames moving with respect to each other in the x direction.
Note that there always exists a reference frame in which the signal is not moving horizontally; i.e., the signal originates and later is at the same x location in that reference frame (we’re speaking of inertial reference frames here). To say it another way, in NM there is always a potential reference frame, which during the time T can move so quickly relative to another reference frame that it spans the horizontal distance x´ during the time T (or length Irel =CT).
This Interval is defined here using NM concepts but it is the same thing as what is called the ‘Relativistic Interval’ Irel in SRT, i.e., the distance a signal travels perpendicular to the relative motion between reference frames. The same numerical value results in SRT or NM.
3.2 The Gamma Factor
I now wish to define another quantity to be called gamma ( . It is the ratio of the total distance the ‘timing’ signal travels in a reference frame to the distance it traveled perpendicular to the relative motion (the perpendicular distance, i.e., the Interval Irel). In Fig. 1, this would be (C´ T)/(CT) or in simple terms of the triangle, H/ Irel, a different length of H for each potential reference frame traveling a different value along the horizontal x axis while the signal went the vertical distance CT (or Irel) in all cases. Later in this paper will be shown to be the same in SRT.
4. A Quantity Different Between NM & SRT
It should be obvious that the timing signal (or anything else) cannot travel the same distance in both of two reference frames moving with respect to each other. It must be admitted that if it moves only vertically in one reference frame, and in another reference frame moves not only that same distance vertically but also moves horizontally, then the distances moved in the two reference frames cannot be the same. In Fig. 1, this would mean C´ T cannot equal CT and this is shown in Eq. 12. This is because x ≠ x´ (and x´ is not equal to x´´, etc.). It is also obvious that the speed C´ and C cannot be the same or the distance the timing signal traveled would be wrong for at least one of the reference frames. Or would it?
Of course, given Eq. (15), making C’ equal to C results in an inequality
(17)
because x=0 and x´ does not. But what if we made the C quantities the same but made the T quantities different? What if we wrote the Interval equation as:
Irel 2 = . . . (18)
This change of Eq. (15) into Eq. (18) to avoid becoming Eq. (17) is the creation of SRT. I will now use lower case letters to denote SRT quantities. See Fig. 2. However, Irel still has the same meaning in both SRT and NM, i.e., the perpendicular distance the timing signal would have in all reference frames, as noted in the triangles of both Fig. 1 and Fig. 2. And still has the same meaning in both SRT and NM: the ratio of the distance the ‘timing’ signal traveled in a reference frame to the perpendicular distance it traveled. Again, in terms of the triangles
Irel (19)
Note well that in doing this I have just made the Assumption (Proposition, Postulate, etc.) that something (anything — the timing signal in this case) can travel the same speed in two reference frames moving with respect to each other. Because x’ could be any value, the ‘proposition’ that the timing signal travels the same speed in two reference frames moving with respect to each other leads to the conclusion that the timing signal travels the same speed in all reference frames. This is Einstein’s Second Postulate. It will be shown later that reference frames always travel at speed less than c with respect to each other. Notice also that what c is, or its value, has not been specified. There is more on this subject later.
Fig. 2. Positions of x=0, x’=0, and 'timing signal' l after time t (=T from Fig. 1) but
holding c (=C from Fig. 1) constant while substituting different times t and t’ for T.
5. Deriving SRT from the Interval Irel
Eq. (18) is all that you need to derive all the equations and concepts of SRT. This is pictured in Fig. 2 which is the same NM physical situation as Fig. 1 except labeled differently by attributing the different distances of H and Irel , not to different velocities of the timing
signal in the two reference frames because of their relative horizontal movement, but rather to different times in the two reference frames. The H and Irel are not equal, and because these distances are the result of a speed multiplied by a time, if you insist that the obviously different speeds c and c´ are equal, then the only option is to claim that the ‘time’ is different in the two reference frames. (Not only that but you also have to have a different time in every location in both reference frames as will be shown.)
However, notice that the SRT quantity that is the SAME as the NM time T is the (Relativistic and Newtonian) Interval Irel divided by c, i.e., (Irel /c). Also, the SRT time in the reference frame where the motion of the timing signal is only perpendicular to and not along the horizontal direction x is what is called in SRT ‘proper time’ and is also the same as Irel /c.
5.1 The Gamma Factor
Above, was defined as the ratio of the distance H to the distance Irel; or ct´/ct; (or C´ T/CT in the NM Fig. 1).
For x=0, Eq (18) becomes
Irel 2 ; (18a)
(20)
Therefore,
(21)
or
(22)
5.2 The Velocity Between Reference Frames
Let x=0 as shown in Figs. 1 & 2. Think of it as a point in the unprimed reference frame. The point x=0 of the unprime reference frame has moved the distance x´ away from x’=0 in the horizontal direction x. Let us define the quantity u as the speed equal to the distance x=0 has traveled horizontally in the prime frame, divided by the time in that reference frame. Therefore,
(23)
(24)
or in terms of the triangle
(25)
Here u is the value used in SRT as the speed between reference frames. It is obviously totally different, qualitatively as well as quantitatively, from the NM velocity between reference frames which is v = x´/t or x´/(Irel /c) = x´/T; and v/c = x’/ct = x´/Irel or in terms of the triangles, L/ Irel in Fig. 2. (If it helps, this would be v = x´/T, and v/c = x’/CT = x’/Irel of Fig. 1 but those are the same quantities as in Fig. 2.)
Substituting the definition of u into Eq. (22)
(26)
and
(1a)
as usually written in SRT. Thus, has the same value in NM and SRT, although it is not used in NM.
5.3 The SRT Transformation Equations
Now let us derive a SRT transform equation. It can be derived from Eq. 18 for x=0 but this is quicker. From Eq. (20)
(20a)
Squaring Eq. (24) yields
(24a)
and multiplying by 1 above,
(27)
(28)
and
[for x=0] (29)
which also equals (u/c)Irel.
The SRT transform equation is generally written
(30)
However, it can be written equally validly and more insightfully as
(31)
where it resembles the NM transform Eq. (5), and in terms of the triangle with x=0,
Irel Irel (32)
in SRT and
Irel) Irel (33)
in NM, i.e., x´ is the same result using Irel and c and the NM velocity ratio v/c = L/Irel, or the SRT ‘velocity’ ratio u/c and . The triangle visualization should help reveal what is occurring; namely, two different systems of outlook describe the same physical situation, which mathematical systems are transformable into each other on a one to one basis.
Eq. (29) is the same as Eq. (31) [and Eq. (30)] except we have not yet included the ‘displacement’ γx, which makes no difference at this point because x=0. The x in Eq. (5) and the x in Eq. (31) and (30) are ‘displacements’ as noted in footnote 2 and for now are considered zero. Thus the point x´=0 has moved the distance x´ in both Fig. 1 and Fig. 2 during the (SRT and NM) Interval ct (or CT).
From Eq . 20, the SRT time transformation for x=0 is
[for x=0] (34)
The full SRT time transform equation is usually written
(35)
This can easily be rewritten
(36)
which is Eq. (34) with an ‘x’ term added. Again, x is a ‘displacement’ value that for now is zero, but will soon be formulated.
5.4 Reverse Transformation Equations
Eqs. 29 and 34 convert SRT distance and time from the unprimed frame to the prime frame for x=0. The SRT equations
(37)
and
(38)
converting from the primed frame to the unprimed for x’=0 can be derived in like manner.
Fig. 3. Positions of x=0, x’=0, and 'timing signal' l rising from x’=0 in the
prime frame after time t’ (=T from Fig. 1 and t from Fig. 2). Distance x = – x’ of Fig. 2.
A perpendicular timing signal l could have been released from x´=0 when x=0 and x´=0 passed each other. Fig. 3 shows this. The prime ‘timing’ signal is perceived by the unprime reference frame just as the unprime ‘timing’ signal was perceived by the prime reference frame except that since the viewpoint is reversed, some quantities become negative.
5.5 Equations Including the ‘displacement’
We still have the task of including the ‘displacement’ x in the equations to come up with Einstein’s SRT transformation equations. One can try simply adding x to Eqs. (29), (34), (37), and (38). However, the result will be the unacceptable inequality
(ct´)2 – x´ 2 ≠ (ct)2 – χ2 . Try it.
The problem of finding the ‘displacement’ x function can be done simply in the following manner.
x´= γ(u/c)ct + ax (39)
x = – γ(u/c)ct´ + bx´ (40)
ct´ = γct + fx (41)
ct = γct´ + hx´ (42)
where a, b, f, and h are yet
to be found.
First let x´=0. Then Eq. (39) becomes
0 = γ(u/c)ct + ax (39a)
and Eq. (42) becomes
ct = γct´ (42a)
and Eq. (39), using Eq. (42a) and (40), becomes
0 = γ2(u/c)ct´+ ax = γγ(u/c)ct´+ a(–)γ(u/c)ct´ (39b)
aγ(u/c)ct´= γγ(u/c)ct´
so a = γ (43)
Now let x=0. Then Eq. (40) becomes
0 = – γ(u/c)ct´+ bx´ (40a)
and Eq. (41) becomes
ct´= γct (41a)
and Eq. (40), using Eq. (41a) and (39), becomes
0 = – γγ(u/c)ct + bγ(u/c)ct (40b)
bγ(u/c)ct = γγ(u/c)ct
so b = γ (44)
The process to find f and h after finding a and b is a little more complex, and will not be shown here. The results are as usual f = γ(u/c) and h= – γ(u/c) .
Therefore, the full SRT transformation equations are:
x´= γ(u/c)ct + γx = γ(x+ut) (45)
x = – γ(u/c)ct´ + γx´ = γ(x´–ut´) (46)
ct´= γct + γ(u/c)x t´= γ[t + (u/c2)x] (47)
ct= γct´ – γ(u/c)x´ t = γ[t´ – (u/c2)x´] (48)
5.6 Comment on ‘Displacement’
In NM, ‘displacement’ is simple. If a railroad engine is half a mile ahead of the caboose in the train reference frame, it is a half mile ahead of the caboose in the ground reference frame. In SRT, the displacement in one reference frame does not equal the same displacement in the other reference frame. Furthermore, when you change the displacement you must also change the time in that reference frame so as to maintain the same SRT (and NM) Interval, or you will not be working with the same events as before. For example, if you change x in Eq. (45) from 0, you will change the value of x´ by x and you will also have to change ct so as to keep Irel 2 = (ct)2 – x2 the same as before.
5.7 Why “Nothing can go faster than c”
Consider the velocity between reference frames in SRT as shown algebraically and in the triangles. The SRT velocity ratio u/c is the ratio of the ‘horizontal’ distance traveled by the reference frame to the distance the timer signal traveled in the same reference frame. Since the signal traveled vertically as well as horizontally, the denominator distance will always be greater and therefore u/c is always less than unity.
This is easily seen in the triangle where
(49)
Note that in NM, velocity ratio v/c is
Irel (50)
or in terms of the triangles,
Irel Irel (51)
which is (u/c). As noted before, this is caused by claiming the difference the timing signal traveled in the two reference frames is not due to the obvious difference in velocity of the timing signal with respect to each of the two ‘moving relative to each other’ reference frames but to different ‘time’ since that is the only variable left to mess with if you wish to keep c the same in both reference frames.
It is important to note that, although u/c is always less than unity, the ratio of the reference frame movement distance x´ to the timer signal distance ct = Irel (constant in all reference frames) is not (u/c) but (u/c) as shown by Eq. (45) (for one point in the unprime frame such as x=0) and L/Irel in terms of the triangles. x´/Irel = x´/ct exceeds 1.0 for any value of (u/c) > 1 ; i.e., the reference frames have moved past each other a distance greater than the ‘timing signal’ has moved perpendicularly for any value of (u/c) >1/ . However, u/c is always less than 1.0, no matter how much x´ exceeds ct = Irel.
5.8 More on ‘Timing Signals’
It is important to understand that the perpendicular ‘timing signal’ that is referred to as speed c can be any constant speed. Everything said so far applies. When the speed is specified, a particular time in the ‘signal’ reference frame results in a known perpendicular distance traveled which is uncontested because there is no relative motion in that direction. It is the total vertical plus horizontal distance between the later location of the ‘signal’ and the zero point of the moving reference frame, which is increased in reference frames moving horizontally. NM attributes it to the greater distance added by the horizontal movement during the time T = Irel/c (Irel being the same in SRT and NM) and SRT simply insists that the vertical versus the same vertical plus horizontal movement should be attributed to a change in time.
Furthermore, the ‘timing signal’ traveling at whatever constant speed c can be anything—or nothing! It simply requires one to specify its characteristics. It can be 300 meters per second or 300 meters per microsecond (the speed of light we get in our earthbound habitat), or anything else. When you substitute Eq. (18) for Eq. (15), SRT results, no matter what value for c is chosen—even 10 miles per hour, as in George Gamow’s “Mr. Tompkins in Wonderland”.
6. SRT Proofs and Other Topics
6.1 Minkowski Spacetime & the SRT (and NM) Interval
Minkowski sort of ‘completed’ SRT by introducing the concept that, unlike in NM, both space and time of events are not constant in different moving reference frames. But in SRT a quantity called spacetime is constant in different moving reference frames. The formula for the spacetime Interval between two events, which is constant in all reference frames, is
(52)
or, put in terms of delta between two points,
(53)
Take the negative, rearrange, and observe that:
(54)
(55)
which is the same as the SRT (and NM) time-like Interval squared
(Irel 2 positive) from Eq. (18) when and equal zero, which can always be accomplished by rotating the coordinate axes so that only the x axis is in the direction of relative motion of the reference frames.
Furthermore, for the reference frame in which ∆x equals zero, the ct direction will be perpendicular to the x direction and, if one desires easier visualization, can be converted to the y direction by rotating the coordinate frame about the x axis until ct has no z component.
The (Irel)2 that was discussed earlier is the same concept as Minkowski’s spacetime. The negative makes no difference. (Irel)2 = – s2. Thus, Minkowski’s spacetime Interval, constant between two events in all reference frames, is the same as the SRT (and NM) time-like Interval (I2 positive), which is the same as Newtonian time T multiplied by c.
6.2 Spacetime is a Surrogate for NM Time
The ‘timing signal’ has been spoken of as the ‘something’ that travels a distance perpendicular to the relative motion of the reference frames at speed c. Earlier it was mentioned that the ‘timing signal’ could be anything, or nothing, as long as ‘it’ had traveled the distance ct at speed c. This is really a surrogate for the Newtonian time—which is equal to the absolute value of the spacetime/c, the SRT (and NM) Irel/c, SRT ‘proper’ time, and Newtonian time, all of which are the same and are constant in all reference frames for two events observed from reference frames moving with respect to each other. NM time is what it was before SRT. Although SRT ‘time’ can be the same as NM time (‘proper time’), it is usually actually a function of NM time and a location (distance) as shown by the definition of Irel , Eq. (18)
Irel2 (18b)
or
(18c)
6.3 Comment on Ritz
At the ver y least, in SRT, electromagnetic radiation such as light must travel from its source at speed c. (SRT also claims of course that electromagnetic radiation is traveling at the same speed c with respect to everything else no matter how ‘everything else’ is moving relative to such sources or to anything else.) Notice that in both Figs. 2 and 3, the ‘timing signal’ (e.g., light) is traveling at ‘speed c from its source’. This is known as the Ritz theory which has supposedly been disproven by astronomical observation.
6.4 Comment on Michelson-Morley
There are several things that presumably proved the correctness of SRT. First, it fit the null result of the Michelson-Morley and similar experiments. However, there are a number of other possible explanations for the null result. These will not be examined now but Petr Beckmann’s “Einstein Plus Two” and Tom Bethell’s “Questioning Einstein”, which is based on the ideas of Petr Beckmann and Dr. Howard Hayden, give excellent possible explanations.
6.5 Comment on GPS
It is sometimes said that if relativistic corrections had not been made to the atomic clocks of the global position system, it would not work. To quote from a website on the subject, “Fact is, it would not matter whether such adjustments were made or not.” The site is:
<http://www.alternativephysics.org/book/GPSmythology.htm>.
So the GPS system is neither a proof nor a disproof of SRT.
6.6 Comment on Hafele-Keating
The 1971 Hafele-Keating (HK) flight of atomic clocks around the world east to west and west to east to detect a difference at which the clocks ran attributable to SRT showed huge variability in the times of the clocks. Some have criticized that even these numbers were ‘adjusted’. So HK is not a proof of SRT.
6.7 Comment on Muons
A presumably strong proof of SRT relates to muons formed in the upper atmosphere by cosmic ray bombardment. Let’s examine muons in the laboratory where they have a known half-life of 2.2 microseconds (mus). We generate them and find that after 2.2 mus half of them have decayed. We know the time was 2.2 mus because we sent a light pulse east and it traveled 660m (2.2 mus) while the decay took place.
Now we created some muons traveling north at a speed such that half the muons decayed after traveling 330 meters during the time the east moving light pulse traveled 660 meters. ct=660m; x´=330m. By SRT,
(45)
Since x=0 (the light pulse is east and the motion is north)
(u/c) = 0.5; = 1.1180; u/c = 0.5/1.1180 = 0.4472.
(47)
ct´ = ct + 0 = 1.1180 * 660m = 737.90m; t´/t = 1.1180
The experiment is repeated with faster muons. This time the point where 50% decay has occurred is 500m. ct=660m; x´=500m; and using the same method as above,
(u/c) = 0.7576; = 1.2546; u/c = 0.6039; ct´ = ct=828.01m; t´/t = 1.2546
The experiment is repeated again with still faster muons. This time the point where 50% decay has occurred is 660m. ct=660m; x´=660m;
(u/c) = 1.000; = 1.4142; u/c = 0.7071; ct´ = 933.38m; t´/t = 1.4142
This has worked so well it should be tried a couple more times. We generate muons moving so fast that we find the point where 50% of them have decayed is 1320m. ct=660m; x’=1320m;
(u/c) = 2.000; = 2.2361; u/c = 0.8944; ct´ = 1475.80m; t´/t = 2.2361
Finally we get equipment that can move the muons so fast that 82% percent have not decayed at 1900m. Normally we expect laboratory muons to decay 50% every 2.2 mus during which the light pulse travels east 660m. By the time the east-moving light pulse has traveled 1900m or 6.33…mus, there should only be 13.6% of the muons left.
The lab muons would decrease to 82% in only 0.630mus, during which the east traveling light would reach 189m. But the cosmic muons went over 10 times as far (1900 meters) while decreasing to 82% of their original number. Irel = ct =189m, x´=1900m.
Quick calculation shows that, since the east moving light has not traveled in the north direction, x=0 and
Irel ] (45a)
(u/c) = x’/ct = L/Irel = v/c = 10.0545; = ct´/ct = H/Irel = 10.1025;
u/c=x´/ct´ = L/H =0.99509; ct’ = 1909.377m; t’/t = H/Irel = 10.1025.
Remembering that Irel and are the same in both NM and SRT and referring to Figs. 1 and 2, one can say for x=0 (the condition where the timing signal is moving only perpendicular to the motion between reference frames):
Irel = ct = CT = 189m;
x’ = L = 1900m;
ct’ = C’ T = 1909.3771m;
u/c = x´/ct’ = L/H = 0.99509;
= ct´/ct = H/Irel = C´ T /Irel = C´ T / C T = 10.1025.
x´ = (v/c) Irel = 10.0529*189m = 1900m
x´ = (u/c)Irel = 10.1025*(0.99509)*189m = 1900m
v/c = x´/Irel = 1900/189 = 10.0529 = (u/c)
Note that since (x´/Irel) = (u/c), x´ can exceed the distance light travels in the perpendicular direction ct = Irel by any amount. Also, the light traveled 1909.377m horizontally and perpendicularly in the muon reference frame while the light traveled only 189m perpendicularly in that frame. The ratio of these two numbers is gamma in both SRT and NM and is 10.1025.
The ratio of the distance traveled by the cosmic muons to the (SRT and NM) Interval Irel, which Interval is constant in all reference frames for any two events, is 10.0529. They traveled 1900m while the light traveled 189m. They traveled 10.05… times the distance the light traveled perpendicularly, yet according to the math of SRT, they traveled at 0.99509 times c. Keeping in mind that Irel/c is the same in NM as SRT, they traveled 1900m in T= Irel/c or 0.630mus which equals 3016m/mus vs. 300m/mus for the perpendicular light.
Rather than a proof of SRT, cosmic muons expose the mathematical gyrations of SRT. In light of understanding the figures, their triangles, the math of SRT, and particularly Eqs. 15, 17, and 18, the idea that the light beams from my flashlights traveling from me at speed c in opposite directions are traveling from each other at speed c is ….[fill in the blank].
And you don’t even have to worry about what a physicist riding one of the high speed muons thinks about the half-life of the laboratory muons!
6.8 SRT, Gravity, & GRT
In General Relativity Theory (GRT) Einstein took into account that light is affected by the mass (gravity) of the sun. This of course would ordinarily be thought of as light’s velocity being affected by gravity. However, since he insisted by SRT that light travels at constant speed c in all reference frames, no matter how these reference frames are moving with respect to each other, it became necessary in GRT to convolute space and time even more rather than acknowledge various effects on light. Dr. Howard Hayden likened this to firing a rifle horizontally on earth, noting that the bullet deviated downward toward the earth and slowed down, and concluding that, since it had previously been postulated and generally accepted that bullets always travel at constant speed in a straight line after leaving the muzzle, it is necessary to do very complicated time and distance corrections to show that this is still so!
6.9 Shapiro Time Delay; Michelson-Gale
The Shapiro time delay implies that gravity caused a time delay. If something is delayed, it is reasonable to assume that the velocity decreased.
The Michelson-Gale experiment showed a fringe shift implying that light did not travel the same speed east/west as west/east, at least not in Colorado. Light traveling near earth at constant velocity relative to the earth gravitational field irrespective of its rotation could explain this.
The importance of these is simply that experiment and observation have shown that light does not always travel at exactly speed c —and speed c relative to different objects moving different speeds in different directions at that. Trying to keep speed exactly c everywhere and always requires bending other concepts all over the place.
6.10 Momentum
Momentum in NM it is p = mv. In SRT it is p = m u.
Irel Irel (56)
Irel Irel Irel (57)
so momentum in both SRT and NM can be written p=mx´/(Irel /c) = mx´/T or in terms of the triangles, m(L/Irel)c.
Kinetic energy is quite different because the integration from momentum is performed on the qualitatively very different velocities v in NM and u in SRT. This has been covered in an article correctly described as “long and boring” which equates SRT changes in rest mass due to motion changes as the equivalent of (not the same values as) potential energy in NM.
Essentially, the article shows kinetic problems are solvable in NM when we know the force (equal and opposite) acting on each object and the time or distance the forces act to get the resultant motion, OR you can get the resultant motion more simply by invoking the concept of conservation of total energy (kinetic plus potential) to solve the problem. In the first case, potential energy is not used; in the second case it is used and changes.
In SRT in kinetic problems, you can describe the forces (equal and opposite) acting on each object and the time or distance the forces act to get the resultant motion without using the concept of rest mass change, OR you can get the resultant motion more simply by invoking the concept of conservation of total energy with kinetic energy to/from rest mass energy changes to solve the problem. Why does rest mass change or not depending on how YOU decide to solve the problem?
7. Conclusion
By ignoring that ‘anything’ traveling a certain speed vertically in a reference frame cannot travel that same speed in another reference frame where it moves the same distance vertically but also horizontally as well, Einstein messed up ordinary concepts of time, distance, and relative velocity. Thus, for a given physical situation, one can either claim that the different distances traveled in the given situation (time) gave the ‘anything’ different velocities in different moving reference frames according to Newtonian Mechanics (NM), or claim that the velocities were the same in the different frames but that the times were different according to Special Relativity Theory (SRT). Exactly how this change in viewpoint from NM to SRT occurs has been presented both analytically and graphically.
When examined, the SRT quantities Interval Irel and are the same in NM, as is also momentum when examined carefully.
A physical situation can be described equally well with SRT or NM because SRT and NM are one to one mathematical transformations of each other as shown. Of course it is much easier to visualize the NM description.
Furthermore, since according to SRT, light travels the same speed in all reference frames, it must travel at speed c from all its sources, no matter how those sources are moving relative to other things, also known as Ritz theory which has presumably been disproved.
There are other explanations of how light travels than ‘constant speed in all reference frames’ that adequately explain the physics. Two books were mentioned which cover this.
The reason ‘nothing can travel faster than light’ is that, in SRT, relative velocity between reference frames u/c is the ratio of the distance the reference frame traveled ‘horizontally’ to the distance light traveled in that same reference frame ‘horizontally’ and, in addition, perpendicularly the distance Irel, a constant in that and all other reference frames, meaning the ratio of a leg of a right triangle to its hypotenuse, which will always be less than unity. This becomes obvious in the graphics presented
Minkowski’s ‘constant in all reference frames’ spacetime is shown to be the same (qualitatively and quantitatively) as a distance equal to ordinary Newtonian time multiplied by c.
All SRT descriptions can be replaced by NM descriptions where distance and time mean concepts with which most people are familiar. This point can be driven home further by an article on the website <trybasics.com> (accessed 2/28/’16) which derives the transform equation of NM only from the SRT transform equations, thus again showing the 1:1 mathematical transformation between the two.
Epilogue
Actually Einstein’s ‘second postulate’ in his 1905 paper was “light is always propagated in empty space with a definite velocity c which is independent of the state of motion of the emitting body”. After completing this paper it suddenly dawned on me that this is a meaningless statement!
When I say, "I am driving in my car at 50 miles per hour”, that is also, strictly speaking, a meaningless statement. Of course, I and everyone else assume that I mean 50 miles per hour relative to the earth’s surface. Velocity is always relative to something. If I am driving east in El Paso, Texas, my speed is also about 930 mph, or if driving west, it is also about 830 mph—backwards—relative to the earth’s axis. Einstein’s postulate says electro-magnetic radiation is “always propagated in empty space with a definite velocity c”, but relative to what? Whether he recognized it or not, his answer in SRT is ‘relative to everything’, which is senseless. That would be like me saying I am driving 50 miles per hour relative to the earth’s surface, the earth’s axis, the moon, Mars, the sun, and the nearest star. Interesting!
A Simple Special Relativity model is offered which easily explains the 'twin paradox', why c is a maximum speed limit, and makes the concept of SR easy to understand.
Dr. Sherwood Kaip
El Paso, TX
Section 5.5, including formulas, is correct in this screen version. Unfortunately, the formulas did not transfer properly so will have to be added eventually. If you click on the print button above you will get the double column print version which is also readable.